Ringkasan
Ahli ekologi dan ahli biologi evolusi mengandalkan seperangkat alat statistik yang semakin canggih untuk menggambarkan sistem alam yang kompleks. Salah satu alat yang telah memperoleh daya tarik signifikan dalam ilmu biologi adalah model persamaan struktural (SEM), suatu bentuk analisis jalur yang menyelesaikan hubungan multivariat yang kompleks di antara serangkaian variabel yang saling terkait.
Evaluasi SEM secara historis bergantung pada kovariansi antar variabel, bukan pada nilai titik data itu sendiri. Meskipun pendekatan ini memungkinkan berbagai macam bentuk model, pendekatan ini membatasi penggabungan spesifikasi terperinci. Perkembangan terkini telah memungkinkan penerapan distribusi non-normal, efek acak, dan struktur korelasi berbeda secara bersamaan menggunakan estimasi lokal, tetapi proses ini belum diotomatisasi dan akibatnya, evaluasi dapat menjadi penghalang dengan model yang kompleks.
Di sini, saya menyajikan paket sumber terbuka yang terdokumentasi lengkap, piecewise SEM, implementasi praktis analisis jalur konfirmatori untuk bahasa pemrograman r . Paket ini memperluas metode ini ke semua model linear (umum), kuadrat terkecil (filogenetik), dan efek campuran saat ini, dengan mengandalkan sintaksis r yang sudah dikenal . Saya juga memberikan dua contoh yang sudah dikerjakan: satu yang melibatkan efek acak dan autokorelasi temporal, dan yang kedua yang melibatkan kontras yang independen secara filogenetik.
Sasaran saya adalah menyediakan implementasi SEM yang mudah digunakan dan mudah dipahami, yang juga merefleksikan proses ekologi dan metodologi dalam menghasilkan data.
“Tidak ada pepatah yang lebih sering diulang sehubungan dengan uji coba lapangan, selain bahwa kita harus mengajukan beberapa pertanyaan kepada Alam, atau, idealnya, satu pertanyaan, pada satu waktu. Penulis yakin bahwa pandangan ini sepenuhnya keliru. Alam, menurutnya, akan merespons dengan lebih baik terhadap kuesioner yang logis dan dipikirkan dengan saksama; sesungguhnya, jika kita mengajukan satu pertanyaan kepadanya, ia akan sering menolak untuk menjawab sampai beberapa topik lain telah dibahas.”
—Tuan Ronald Fisher (1926)
Perkenalan
The desire to understand the intricate complexity of nature is arguably the single driving force behind all of science. Yet, for the last century or so, ecologists and evolutionary biologists have closely examined the impact of one or few factors on a single response. This practice was, and sometimes still is, a consequence of limited computational power, and the necessity of simplification in rigorous experimentation. However, with the advent of modern computing and the tractability of large-scale observation, there is an increasing recognition that multifaceted data sets representing complex natural systems require an equally sophisticated toolbox. Structural equation models (SEM) provide one such tool.
Structural equation models are probabilistic models that unite multiple predictor and response variables in a single causal network. They are often represented using path diagrams, where arrows indicate directional relationships between observed variables (Figs 1 and 2). These relationships can be captured in a series of structured equations that correspond to the pathways in the model. Two primary characteristics of SEMs separate them from more traditional modelling approaches:
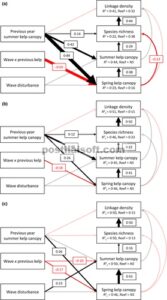
Model persamaan struktural (SEM) dari Byrnes et al . ( 2011 ) mengeksplorasi efek frekuensi badai (gangguan gelombang) pada struktur komunitas hutan rumput laut dan kompleksitas jaring makanan (kepadatan hubungan). Kotak mewakili variabel yang diukur. Anak panah mewakili hubungan searah di antara variabel. Anak panah hitam menunjukkan hubungan positif, dan anak panah merah menunjukkan hubungan negatif. Anak panah untuk jalur yang tidak signifikan ( P ≥ 0·05) bersifat semi-transparan. Ketebalan jalur yang signifikan telah diskalakan berdasarkan besarnya koefisien regresi terstandarisasi, yang diberikan dalam kotak terkait. R 2 s untuk model komponen diberikan dalam kotak variabel respons (untuk panel b dan c, ini dilaporkan sebagai kondisional guci:x-wiley:2041210X:media:mee312512:mee312512-matematika-0001berdasarkan varians efek tetap dan acak). Variabel ‘Habitat terumbu karang’ telah dihilangkan demi kejelasan dan koefisien jalur malah dilaporkan dalam kotak respons yang sesuai, seperti dalam Byrnes et al . ( 2011 ) (NS = tidak signifikan). (a) Analisis asli menggunakan SEM varians–kovarians. (b) Model yang sama dalam model yang dipasang menggunakan SEM sepotong-sepotong dan menggabungkan efek acak dari Lokasi . (c) Model sepotong-sepotong dari panel b, dengan istilah autokorelasi tambahan untuk Tahun .
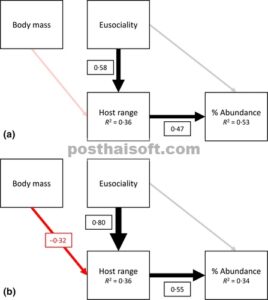
Model persamaan struktural (SEM) yang diturunkan dari hipotesis dalam Duffy & Macdonald ( 2010 ) yang mengeksplorasi hubungan di antara eusosialitas, ukuran tubuh, ukuran jangkauan inang, dan kelimpahan regional proporsional untuk udang Synalpheus yang eusosial . Anak panah menggambarkan hubungan searah di antara variabel. Anak panah hitam menunjukkan hubungan positif, dan anak panah merah menunjukkan hubungan negatif. Anak panah untuk jalur yang tidak signifikan ( P ≥ 0·05) bersifat semi-transparan. Ketebalan jalur signifikan telah diskalakan berdasarkan besarnya koefisien regresi terstandarisasi, yang diberikan dalam kotak terkait. R 2 untuk model komponen diberikan dalam kotak variabel respons. (a) Analisis menggunakan SEM varians–kovarians. (b) Model yang sama seperti pada kecocokan menggunakan SEM sepotong-sepotong, dan juga menggabungkan struktur korelasi tetap berdasarkan jarak filogenetik yang diperoleh dari filogeni molekuler.
Jalur menggambarkan hubungan kausal yang dihipotesiskan . Ini adalah penyimpangan dari frasa, ‘korelasi tidak menyiratkan kausalitas.’ Faktanya, korelasi memang menyiratkan kausalitas, tetapi arah kausalitas tidak terselesaikan, karena seseorang tidak dapat mengetahui apakah, misalnya, A menyebabkan B, B menyebabkan A, atau A dan B keduanya merupakan konsekuensi dari beberapa variabel ketiga yang tidak terukur (Shipley 2000b ). Namun, dengan menggunakan pengetahuan yang telah ada sebelumnya tentang sistem yang diperoleh melalui observasi dan/atau eksperimen, seseorang dapat membuat hipotesis yang terinformasi tentang struktur kausal A, B, dan variabel lain yang dianggap memediasi hubungan mereka. SEM memungkinkan pengujian langsung dari struktur kausal yang seharusnya ini. Dengan cara ini, SEM merupakan penyimpangan dari pemodelan linier tradisional dengan secara eksplisit menguji hipotesis bahwa A menyebabkan B. Sementara pembahasan mendalam tentang ide ini berada di luar cakupan makalah ini, pembahasan lebih lanjut tentang kausalitas dan bagaimana kaitannya dengan SEM dapat ditemukan di: Pearl ( 2012 ) dan Bollen & Pearl ( 2013 ).
Variabel dapat muncul sebagai prediktor dan respons . Dengan memungkinkan satu variabel berfungsi sebagai respons dalam satu jalur dan sebagai prediktor di jalur lain, SEM berguna untuk menguji dan mengukur efek tidak langsung atau berjenjang yang jika tidak demikian tidak akan dikenali oleh model tunggal mana pun (misalnya Grace et al . 2007 ).
Model persamaan struktural menuntut perubahan dalam cara pertanyaan ekologi dan evolusi disusun dan diuji, dengan penekanan pada evaluasi simultan dari beberapa hipotesis kausal dalam satu jaringan.
Secara historis, SEM telah diestimasi menggunakan pendekatan kemungkinan maksimum untuk memilih nilai parameter yang paling baik mereproduksi keseluruhan matriks varians–kovarians yang diamati. Kebaikan kesesuaian SEM kemudian dapat dievaluasi menggunakan uji chi-kuadrat yang membandingkan estimasi dengan matriks kovariansi yang diamati (Grace 2006 ). Namun, pendekatan ini mengasumsikan bahwa semua observasi bersifat independen, dan semua variabel mengikuti distribusi normal (multivariat) (Grace 2006 ). Pendekatan ini juga membatasi jumlah minimum observasi yang diperlukan untuk menyesuaikan SEM, karena harus ada derajat kebebasan yang cukup untuk memperkirakan keseluruhan matriks varians–kovarians (aturan ‘ t ‘, Grace 2006 ).
Pembatasan ini mengarah pada pengembangan paralel dari SEM asiklik terarah, atau sepotong-sepotong, berdasarkan aplikasi dari teori grafik. Dalam SEM sepotong-sepotong, diagram jalur diubah menjadi serangkaian persamaan linear (terstruktur), yang kemudian dievaluasi secara individual. Peralihan dari estimasi global , di mana persamaan diselesaikan secara bersamaan, ke estimasi lokal , di mana setiap persamaan diselesaikan secara terpisah, memungkinkan pemasangan berbagai macam distribusi dan desain pengambilan sampel (Shipley 2000a , 2009 ). Secara teori, hal ini juga memungkinkan pemasangan set data yang lebih kecil, karena hanya perlu ada derajat kebebasan yang cukup untuk memasang model komponen apa pun (Shipley 2000a ) (tetapi lihat 5 : 5.2 ). Akhirnya, hal ini dapat menggabungkan jarak yang diperoleh dari taksonomi atau filogeni untuk mengatasi efek yang berpotensi membingungkan dari sejarah evolusi bersama (Von Hardenberg & Gonzalez-Voyer 2013 ). Karena SEM sepotong-sepotong belum menyertakan variabel laten atau komposit, maka SEM ini sering dan lebih tepat disebut sebagai analisis jalur konfirmatori. Namun, saya akan tetap menyebutnya secara luas sebagai SEM sensu Grace et al . ( 2012 ), yang memasukkan estimasi lokal dalam definisi mereka tentang ‘SEM generasi ketiga.’
Karena SEM sepotong-sepotong tidak menghasilkan matriks kovariansi global yang valid, uji kesesuaian alternatif diperlukan. Pendekatan tipikal menggunakan uji pemisahan terarah Shipley . Prosedur ini menguji asumsi bahwa semua variabel bersifat independen bersyarat. Dalam istilah yang paling sederhana, independensi bersyarat menyiratkan bahwa tidak ada hubungan yang hilang di antara variabel yang tidak terhubung (Shipley 2000a ). Langkah pertama dalam uji pemisahan langsung adalah memperoleh set minimum klaim independensi bersyarat yang terkait dengan diagram jalur yang dihipotesiskan, yang dikenal sebagai set basis . Set basis dapat diterjemahkan ke dalam satu set persamaan linier, yang masing-masing dapat dipecahkan seperti model linier lainnya. Signifikansi klaim independensi yang diberikan, yaitu nilai- P -nya , dapat diperkirakan dan diekstraksi. Uji pemisahan terarah dilakukan dengan menggabungkan semua nilai- P di seluruh set basis dalam statistik uji, Fisher’s C , menggunakan persamaan berikut:
guci:x-wiley:2041210X:media:mee312512:mee312512-matematika-0002
(persamaan 1)
di mana P i adalah klaim independensi ke-i dalam basis set yang terdiri dari k klaim. C kemudian dapat dibandingkan dengan distribusi chi-kuadrat dengan 2 k derajat kebebasan. Hubungan yang dihipotesiskan dianggap konsisten dengan data ketika ada dukungan lemah untuk jumlah klaim independensi bersyarat, yaitu ketika kumpulan hubungan tersebut yang direpresentasikan oleh C dapat dengan mudah terjadi secara kebetulan, dalam hal ini P untuk uji chi-kuadrat lebih besar dari ambang signifikansi yang dipilih (biasanya α = 0·05). Beberapa contoh yang mudah dipahami dari derivasi basis set dapat ditemukan di Shipley ( 2000a , 2009 ).
Shipley ( 2013 ) menunjukkan bahwa statistik Fisher C dapat digunakan untuk mendapatkan nilai kriteria informasi Akaike (AIC) menggunakan persamaan berikut:
guci:x-wiley:2041210X:media:mee312512:mee312512-matematika-0003
(persamaan 2)
di mana C berasal dari persamaan 1 , dan K adalah derajat kebebasan kemungkinan (jangan disamakan dengan k , jumlah klaim independensi dalam basis set). Karena estimator ini tidak diturunkan dari kemungkinan maksimum, ia terkadang disebut sebagai kriteria informasi statistik C (CIC, sensu Cardon et al . 2011 ). Persamaan persamaan 2 juga dapat diperluas ke ukuran sampel kecil (AIC c ), biasanya ketika jumlah parameter melebihi ukuran sampel total n /40, dengan koreksi tambahan: AIC c = C + 2 K ( n / n − K − 1).
Implementasi piecewise SEM dibatasi oleh spesifikasi dan evaluasi yang benar dari basis set, yang dapat menjadi mahal untuk diperoleh dengan tangan, terutama untuk model yang sangat kompleks. Untuk tujuan itu, saya menyediakan paket piecewise SEM yang terdokumentasi sepenuhnya dan open-source ( https://github.com/jslefche/piecewiseSEM ) untuk bahasa statistik r untuk membantu dalam perhitungan piecewise SEM dengan membangun basis set, melakukan uji kebaikan-kesesuaian untuk model penuh dan komponen, menghitung skor AIC, mengembalikan estimasi parameter (berskala), memplot korelasi parsial, dan menghasilkan prediksi. SEM dibangun menggunakan daftar persamaan terstruktur, yang dapat ditentukan menggunakan fungsi pemodelan linier paling umum di r , dan dengan demikian dapat mengakomodasi distribusi non-normal, struktur hierarkis, dan prosedur estimasi yang berbeda. Dalam makalah ini, saya menyajikan dua contoh yang dikerjakan: yang pertama menggabungkan model efek campuran dan pengamatan berkorelasi temporal, dan yang kedua melibatkan non-independensi melalui kontras filogenetik independen. Data dan kode r untuk mereproduksi semua analisis diberikan dalam Informasi pendukung.
Contoh 1: Frekuensi badai dan jaring makanan hutan rumput laut
Dalam contoh pertama ini, saya menggunakan data dari Byrnes et al . ( 2011 ), yang meneliti peran peristiwa badai pada keanekaragaman dan struktur jaring makanan hutan rumput laut di California, AS. Mereka menggabungkan survei biologis hutan rumput laut di 35 lokasi berbeda dan 8 tahun, potensi hubungan jaring makanan yang diperoleh dari literatur, data tentang tinggi dan periode gelombang dari stasiun pemantauan fisik, dan tutupan tajuk rumput laut dari citra satelit. Mereka meringkas variabel-variabel ini dalam jaringan kausal tunggal yang diperoleh menggunakan pengetahuan apriori tentang sistem dan hasil dari manipulasi eksperimental (Gbr. 1 ). Mereka kemudian mengevaluasi model ini menggunakan SEM varians–kovarians tradisional.
Byrnes dkk . berhipotesis bahwa gangguan gelombang yang dihasilkan oleh badai musim dingin akan bergantung pada jumlah rumput laut yang ada, yang secara interaktif memengaruhi tutupan tajuk musim semi. Tutupan tajuk musim semi pada gilirannya akan menginformasikan tutupan tajuk musim panas, yang juga tunduk pada pemaksaan fisik. Jumlah tutupan tajuk, musim semi atau musim panas, akan menyediakan habitat struktural bagi berbagai spesies, seperti alga, invertebrata yang tidak bergerak, dan konsumennya. Kekayaan spesies total akhirnya akan menentukan jumlah mata rantai trofik potensial dalam jaring makanan yang diamati (kepadatan mata rantai, atau jumlah rata-rata mata rantai makan per spesies yang diamati).
Hasil analisis asli mereka direproduksi dalam Gambar 1a menggunakan paket lavaan (Rosseel 2012 ). Model tersebut cukup sesuai dengan data berdasarkan keluaran dari uji kesesuaian chi-kuadrat ( guci:x-wiley:2041210X:media:mee312512:mee312512-matematika-0004 = 8,784, P = 0,118). Byrnes et al . ( 2011 ) melihat bahwa tutupan tajuk musim semi sangat dipengaruhi oleh interaksi antara gangguan gelombang dan tutupan rumput laut sebelumnya: seiring meningkatnya tutupan tahun sebelumnya, efek gangguan gelombang pada tutupan tajuk musim semi saat ini menjadi lebih negatif. Tutupan tajuk musim semi memiliki efek negatif langsung pada kekayaan spesies, dan efek positif tidak langsung yang dimediasi melalui tutupan rumput laut musim panas. Kekayaan spesies pada gilirannya meningkatkan kompleksitas jaring makanan. Akan tetapi, mereka mencatat bahwa efek negatif langsung dari tutupan tajuk musim semi terhadap kekayaan spesies memiliki besaran yang lebih besar (β terstandarisasi = −0·23) daripada efek tidak langsung, yang diperoleh dengan mengalikan koefisien jalur (0·38 × 0·29 = 0·11). Dengan demikian, mereka menyimpulkan bahwa hilangnya tajuk musim semi akibat badai musim dingin sebenarnya meningkatkan kekayaan spesies (dengan mengurangi efek negatif langsung yang lebih kuat), yang pada akhirnya meningkatkan kompleksitas jaring makanan dalam jangka pendek. Akan tetapi, mengingat efek hilangnya rumput laut, kekayaan spesies total seharusnya menurun jika terumbu karang mengalami gangguan gelombang selama beberapa tahun berturut-turut.
Analisis mereka, bagaimanapun, memperlakukan setiap observasi sebagai independen. Pada kenyataannya, situs yang berdekatan cenderung memiliki karakteristik yang sama, dan dalam satu situs, observasi yang lebih dekat dalam waktu cenderung lebih mirip daripada yang lebih jauh. Untuk mengatasi kedua masalah ini, saya menyesuaikan kembali model asli mereka menggunakan SEM sepotong-sepotong. Dalam analisis ulang pertama, saya mengatasi non-independensi situs pengambilan sampel dengan menyesuaikan setiap respons ke model efek campuran linier umum menggunakan fungsi lme dari paket nlme (Pinheiro et al . 2013 ). Saya memilih untuk mengubah log variabel seperti pada Byrnes et al . ( 2011 ) alih-alih menyesuaikan respons integer ke distribusi Poisson untuk memfasilitasi perbandingan langsung dengan analisis asli, meskipun ini dimungkinkan menggunakan SEM sepotong-sepotong . Untuk setiap model komponen, saya menyesuaikan efek acak Situs dan hanya mengizinkan intersepnya untuk bervariasi. Saya kemudian menambahkan model komponen ke dalam daftar dan meneruskan daftar tersebut ke fungsi sem.fit , yang mengembalikan pengujian pemisahan terarah, statistik Fisher’s C , dan nilai AIC untuk SEM. Saya kemudian memulihkan koefisien regresi terstandarisasi (diskalakan berdasarkan mean dan varians, seperti dalam Byrnes et al .) menggunakan fungsi sem.coefs .
SEM sepotong-sepotong berdasarkan model campuran mereproduksi data sama baiknya dengan output dari lavaan , berdasarkan perbandingan statistik C Fisher dengan distribusi chi-kuadrat ( C10 = 15·64, P = 0·11). Hasil dari analisis ulang ini diberikan dalam Gambar 1b . Secara umum, model menjelaskan proporsi varians yang lebih besar secara rata-rata daripada SEM tradisional, berdasarkan nilai R2 yang diperoleh dari varians efek tetap dan acak (Nakagawa & Schielzeth 2012 ) , yang diperoleh dengan menggunakan fungsi sem.model.fits .
Ada beberapa perbedaan utama antara model-model dalam Gambar 1 a,b. Pertama, besarnya efek utama dari tutupan tajuk rumput laut tahun sebelumnya dan interaksi antara variabel ini dan gangguan gelombang keduanya berkurang sekitar dua pertiga, meskipun mereka mempertahankan tanda-tanda yang sama. Yang paling penting untuk interpretasi asli adalah bahwa hubungan negatif antara tutupan tajuk musim semi dan kekayaan spesies tidak signifikan. Dengan pengamatan bersarang berdasarkan struktur hierarkisnya, variasi yang sebelumnya diasumsikan dihasilkan oleh tutupan tajuk dialokasikan kembali ke variasi acak (spasial). Dengan demikian, berdasarkan keluaran dari SEM sepotong-sepotong, gangguan gelombang baik secara langsung maupun tidak langsung mengurangi tutupan tajuk musim semi, yang secara tidak langsung mengurangi kompleksitas jaring makanan sebagai akibat dari hubungan positif yang berjenjang antara tutupan tajuk musim semi dan musim panas, tutupan tajuk musim panas dan kekayaan spesies, dan akhirnya kekayaan spesies dan kepadatan tautan.
Dalam analisis ulang kedua, saya membahas baik non-independensi situs maupun potensi autokorelasi temporal dengan mempertahankan struktur acak yang sama seperti di atas, dan sebagai tambahan memodelkan korelasi di antara tahun pengambilan sampel menggunakan struktur autokorelasi autoregresif kontinu 1 dari fungsi CAR1 dari paket nlme (Pinheiro et al . 2013 ). Analisis ini juga mereproduksi data dengan baik berdasarkan perbandingan statistik C Fisher dengan distribusi chi-kuadrat ( C8 = 7 ·84, P = 0·45). Hasil dari analisis ulang ini diberikan dalam Gambar 1c .
Ada sedikit lebih banyak varians yang dijelaskan untuk setiap model komponen vs. SEM sepotong-sepotong tanpa struktur autokorelasi. Namun, ada lebih sedikit perbedaan penting antara dua model sepotong-sepotong. Jalur antara tutupan tajuk musim semi dan kekayaan spesies masih tidak signifikan. Sekarang ada jalur positif yang signifikan antara tutupan tajuk musim panas dan gangguan gelombang, dan jalur yang sebelumnya signifikan antara tutupan tajuk tahun sebelumnya dan kekayaan spesies sekarang tidak signifikan. Namun, perbandingan dua SEM sepotong-sepotong menggunakan AIC mengungkapkan bahwa model yang juga menggabungkan struktur autokorelasi CAR1 adalah model yang jauh lebih kecil kemungkinannya daripada model yang hanya memiliki struktur acak hierarkis (AIC c = 97,69 cf . 81,44).
Singkatnya, analisis ulang ini telah mengungkapkan bahwa pemodelan struktur hierarkis data mengarah pada interpretasi yang berbeda dari data asli: gangguan gelombang mengurangi kompleksitas jaring makanan, terutama dengan menghilangkan habitat. Namun, interpretasi ini mendukung kesimpulan keseluruhan dari Byrnes et al . ( 2011 ) bahwa peristiwa badai (berulang) (yaitu gangguan gelombang) harus mengurangi kompleksitas jaring makanan, meskipun saya menunjukkan efek ini dimediasi melalui penghilangan habitat pada kejadian pertama gangguan dan tidak selalu penurunan kekayaan spesies setelah peristiwa gangguan berulang, seperti yang disarankan oleh Byrnes et al . ( 2011 ). Selain itu, perbandingan model AIC mengungkapkan bahwa pemodelan potensi autokorelasi temporal tidak menambah kemampuan kita untuk memahami sistem interaksi ini.
Eksplorasi lebih lanjut dari model-model dari Byrnes et al . ( 2011 ) yang menguraikan kekayaan spesies total menjadi komponen-komponen trofik mengungkapkan bahwa tutupan tajuk secara signifikan mengurangi kekayaan spesies alga tetapi tidak kekayaan spesies invertebrata yang tidak bergerak atau konsumen yang bergerak, seperti dalam analisis asli mereka (lihat kode suplemen). Pemodelan efek acak dari Situs kemungkinan menyerap beberapa variasi dalam situs yang kaya alga vs. miskin alga, membuatnya lebih sulit untuk melihat kontribusi kekayaan alga terhadap kekayaan spesies total dalam model sepotong-sepotong yang lebih sederhana (Gbr. 1 b,c). Analisis tambahan ini mengonfirmasi bahwa eksplorasi yang lebih dalam oleh Byrnes et al . ( 2011 ) dibenarkan untuk merekonsiliasi keluaran statistik dengan biologi sistem.
Contoh 2: Eusosialitas dan keberhasilan ekologi pada udang penghuni spons
Dalam contoh kedua ini, saya menggunakan data populasi dan ekologi dari genus udang penghuni spons ( Synalpheus ) untuk mengeksplorasi pendorong keberhasilan ekologis. Spesies dalam genus ini menunjukkan berbagai struktur sosial, dari yang berpasangan hingga yang benar-benar eusosial, dengan satu betina yang bereproduksi per koloni. Telah dihipotesiskan bahwa struktur sosial yang kompleks seperti yang ditunjukkan oleh spesies Synalpheus tertentu secara ekologis menguntungkan dalam mendorong kemampuan kompetitif yang lebih besar dan/atau perolehan sumber daya. Untuk menjawab pertanyaan ini, Duffy & Macdonald ( 2010 ) menyusun data tentang massa tubuh betina, jumlah spesies inang yang digunakan (kisaran inang), dan kelimpahan regional proporsional untuk 20 spesies Synalpheus di Belize. Mereka juga menghitung indeks eusosialitas untuk setiap spesies. Mereka berhipotesis bahwa spesies yang lebih eusosial (yaitu koloni yang lebih besar dengan satu betina yang berkembang biak) akan menempati kisaran inang yang lebih luas, yang akan mengarah pada keberhasilan yang lebih besar dalam mempertahankan inang tersebut (yaitu mencapai kelimpahan relatif yang lebih tinggi di area studi). Mereka juga berhipotesis bahwa pengaruh jangkauan inang mungkin dipengaruhi oleh ukuran tubuh, karena sebagian besar spesies eusosial bertubuh kecil.
Sebagai langkah pertama, saya menyesuaikan SEM tradisional menggunakan fungsi sem dari paket lavaan (Rosseel 2012 ), dengan asumsi independensi di antara semua 20 titik data (spesies). Model mereproduksi data dengan baik ( guci:x-wiley:2041210X:media:mee312512:mee312512-matematika-0005 = 0,653, P = 0,419), dan hasilnya diberikan dalam Gambar 2 a. Ada dua jalur minat yang signifikan: efek positif yang kuat dari eusosialitas pada jangkauan inang yang memperhitungkan massa tubuh (β standar = 0,58), dan efek positif dari jangkauan inang dan kelimpahan relatif (0,47). Namun, tidak ada hubungan langsung yang signifikan antara eusosialitas dan kelimpahan. Dengan demikian, tampaknya keberhasilan spesies eusosial sebagian besar merupakan konsekuensi dari kemampuan mereka untuk menempati berbagai inang. Karena penggunaan habitat generalis ini, mereka kemudian juga membentuk persentase yang lebih besar dari total kelimpahan regional, tetapi model tersebut tidak mendukung hipotesis bahwa eusosialitas memberikan keuntungan langsung dalam mempertahankan dan mempertahankan sumber daya habitat tertentu.
Tentu saja, Duffy & Macdonald ( 2010 ) dengan tepat menunjukkan bahwa titik data tidak independen karena beberapa spesies lebih terkait daripada yang lain. Untuk mengatasi masalah ini, saya menyesuaikan kembali SEM pada Gambar 1a tetapi juga memperbaiki matriks korelasi model berdasarkan jarak genetik yang diturunkan dari filogeni Synalpheus di wilayah tersebut (Hultgren & Duffy 2012 ). Saya memperoleh korelasi model dari pohon filogenetik menggunakan fungsi corBrownian dari paket ape (Paradis, Claude & Strimmer 2004 ), dan menyesuaikan model komponen menggunakan fungsi gls dari paket nlme (Pinheiro et al . 2013 ). Saya menyimpan model komponen dalam daftar dan kemudian mengevaluasi SEM menggunakan sem.fit. Seperti sebelumnya, model mereproduksi data dengan baik ( C 8 = 0·57, P = 0·751), dan hasilnya diberikan dalam Gambar 2 b.
Perbedaan mencolok antara dua SEM pada Gambar 2 adalah bahwa SEM filogenetik memulihkan efek negatif signifikan dari massa tubuh pada jangkauan inang (−0·32), mendukung ekspektasi bahwa ukuran tubuh memiliki pengaruh pengganggu. Bahkan di hadapan efek ukuran tubuh, ada efek positif signifikan dari eusosialitas pada jangkauan inang (sebenarnya jauh lebih kuat: 0·80). Seperti pada SEM sebelumnya (Gambar 1 a), tidak ada efek langsung dari eusosialitas pada kelimpahan regional proporsional. Sekali lagi, hubungan ini dimediasi melalui peningkatan jangkauan inang. Mengulangi analisis ini menggunakan fungsi pgls dari paket caper (Orme et al . 2013 ), yang memperkirakan parameter skala tambahan λ, menghasilkan hasil yang hampir identik (lihat kode suplemen).
Dalam paper asli mereka, Duffy & Macdonald ( 2010 ) menggunakan regresi linier berganda untuk mengeksplorasi hubungan di antara keempat variabel ini. Dalam analisis mereka, mereka menunjukkan bahwa eusosialitas memiliki hubungan positif yang kuat dengan kelimpahan relatif dan ukuran jangkauan inang, setelah memperhitungkan perbedaan dalam ukuran tubuh dan sejarah evolusi bersama. Di sini, dalam analisis ulang data mereka menggunakan SEM, saya menunjukkan hubungan antara eusosialitas dan kelimpahan relatif tidak langsung, tetapi lebih merupakan konsekuensi tidak langsung dari menempati lebih banyak inang, wawasan yang tidak mungkin disimpulkan dari regresi berganda individual. Perluasan metode filogenetik ke SEM memfasilitasi pengujian hipotesis multivariat yang lebih kompleks dalam ekologi evolusi dan, seperti yang ditunjukkan di sini, dapat menghasilkan wawasan tambahan yang substansial.
Diskusi
Dalam makalah ini, saya secara singkat memperkenalkan konsep di balik piecewise SEM, dan menerapkan piecewise SEM pada dua analisis yang ada. Dalam kedua kasus, mengakui non-independensi titik data dengan menggabungkan variasi acak atau jarak filogenetik menghasilkan inferensi yang jauh berbeda dari regresi berganda atau bahkan SEM varians-kovarians tradisional. Saya juga menunjukkan bagaimana paket r baru , piecewise SEM, dapat digunakan untuk mengimplementasikan estimasi lokal yang kompleks dengan cepat dan mudah. Memang, paket ini telah digunakan untuk mengeksplorasi pendorong planet dari fungsi ekosistem di hamparan lamun (Duffy et al . 2015 ), mengurai pengaruh keragaman fungsional di seluruh tingkat trofik dalam mesocosms estuari eksperimental (Lefcheck & Duffy 2015 ) dan mengukur pendorong biotik dan abiotik dari multifungsi padang rumput (Jing et al . 2015 ).
Aplikasi yang Lebih Luas
Paket SEM piecewise berisi sejumlah fungsi tambahan yang mungkin menarik bagi pengguna secara umum. sem.model.fits, misalnya, menghasilkan nilai R2 , pseudo- R2 dan AIC untuk model komponen berdasarkan metode dalam Nakagawa & Schielzeth ( 2012 ) dan Johnson ( 2014 ). sem.predict adalah pembungkus untuk fungsi predict generik, dan sebagai tambahan mengimplementasikan standar error pada prediksi dari model yang dibangun menggunakan lme(r) berdasarkan varians efek tetap saja http://glmm.wikidot.com/faq ), meskipun pendekatan ini kontroversial karena tidak memperhitungkan ketidakpastian efek acak, dan dengan demikian, estimasi kesalahan pada prediksi dari model campuran harus ditafsirkan dengan hati-hati. partial.resid mengembalikan plot korelasi parsial antara dua variabel dalam satu model yang memperhitungkan efek kovariat, dan merupakan cara intuitif untuk memvisualisasikan efek parsial yang dikembalikan dari sem.coefs atau, lebih umum, summary . Eksplorasi korelasi parsial juga memungkinkan identifikasi hubungan nonlinier yang sebelumnya tidak dikenali, yang kemudian dapat dimasukkan ke dalam struktur model.
Keterbatasan
Meskipun telah disarankan bahwa SEM sepotong-sepotong dapat digunakan untuk menghindari pembatasan pada ukuran sampel (Shipley 2000a ), penting untuk dicatat bahwa ukuran sampel yang kecil mungkin masih memiliki konsekuensi yang parah untuk analisis. Secara khusus, pengujian pemisahan terarah dapat mendukung ‘model yang pas’ hanya karena pengujian tersebut tidak memiliki daya yang cukup untuk menolak nol (yaitu nilai- P untuk jalur yang hilang semuanya >0·05). Hasil ini akan semakin umum karena model meningkat dalam kompleksitas, tetapi tidak replikasi. Idealnya, penyelidik harus merancang model yang dihipotesiskan sebelumnya dan menggunakannya untuk menginformasikan pengumpulan data, memastikan replikasi yang cukup sejak awal. Sebagai aturan umum, Grace, Scheiner & Schoolmaster ( 2015 ) mengusulkan bahwa rasio jumlah total sampel terhadap jumlah variabel ( d ) tidak boleh jatuh di bawah d = 5. Penting juga untuk memeriksa kecocokan model komponen: jika SEM keseluruhan memiliki kecocokan yang memadai tetapi model komponen memiliki daya penjelasan yang rendah, maka tidak dapat diterima (atau sangat berguna) untuk menarik kesimpulan dari SEM. Akhirnya, pengguna mungkin menemukan diri mereka dengan masalah yang berlawanan, di mana ukuran sampel yang besar mendorong signifikansi statistik tetapi tidak biologis, yang mengarah pada penolakan basis set atas dasar ukuran efek yang tidak penting secara biologis. Dalam hal ini, menerapkan cut-off yang lebih ketat untuk signifikansi statistik dapat mengatasi masalah tersebut.
Perlu dicatat juga bahwa nilai- P yang diperoleh dari paket lmertest (Kuznetsova, Brockhoff & Christensen 2013 ) agak tidak stabil pada saat penulisan, dan sering kali dapat menyebabkan kesalahan dalam fungsi sem.fit . Estimasi dari nlme tampaknya lebih andal, dan saya sarankan pengguna untuk membuat model mereka menggunakan nlme saat lmertest menghasilkan kesalahan, dengan asumsi respons terdistribusi normal.
Sementara pendekatan SEM sepotong-sepotong mewakili lompatan maju yang cukup besar dalam menangani asumsi data dunia nyata, masih dalam tahap awal dibandingkan dengan SEM tradisional telah menyebabkan beberapa keterbatasan. Misalnya, tidak ada implementasi nyata dari kesalahan berkorelasi: hubungan yang bersifat dua arah dan diasumsikan disebabkan oleh pendorong dasar yang sama. SEM sepotong-sepotong mengimplementasikan perkiraan kasar dari kesalahan berkorelasi dengan memungkinkan pengguna untuk mengecualikannya dari set basis (karena tidak ada arah kausalitas yang diasumsikan), dan kemudian menjalankan uji signifikansi sederhana pada korelasi bivariat; namun, metode lain telah diusulkan (Shipley 2003 ), dan dapat dimasukkan dalam iterasi mendatang. SEM sepotong-sepotong juga tidak dapat mengurai hubungan siklik (misalnya A → B → C → A), sehingga tidak mungkin untuk mengevaluasi umpan balik (Shipley 2009 ). Demikian pula, metode ini tidak dapat mengevaluasi hubungan timbal balik dalam model yang sama (A → B dan B → A, jangan sampai tertukar dengan panah dua arah yang menunjukkan kesalahan berkorelasi). Akhirnya, belum ada integrasi formal variabel laten – variabel yang tidak diukur secara langsung, tetapi disimpulkan melalui kombinasi variabel yang diamati (Grace 2006 ) – ke dalam SEM sepotong-sepotong. Dimungkinkan untuk memperoleh prediksi yang mendekati variabel laten menggunakan analisis faktor eksploratori, atau melalui penerapan estimasi MCMC. Namun, belum ada investigasi dan penerapan analisis faktor yang menyeluruh pada SEM sepotong-sepotong. Dengan keberuntungan, perkembangan di masa depan akan melonggarkan beberapa keterbatasan ini.
Ucapan Terima Kasih
Saya berterima kasih kepada JEK Byrnes, JE Duffy, dan KM Hultgren atas kemurahan hati mereka dalam membagikan data yang digunakan dalam makalah ini, dan J Grace, JEKB, JED, A von Hardenberg, dan seorang pengulas anonim yang telah memberikan komentar pada versi awal naskah ini. Terakhir, saya berterima kasih kepada banyak individu, termasuk mereka yang disebutkan di atas, yang telah membantu dalam pengembangan dan pengujian paket SEM sepotong-sepotong . Catatan khusus: N Deguines, TM Anderson, dan T Mason. Makalah ini merupakan kontribusi no. 3512 dari Virginia Institute of Marine Science.
Aksesibilitas data
Semua data tersedia dalam Informasi Pendukung. Versi terbaru piecewise SEM dapat ditemukan di CRAN ( https://cran.r-project.org/web/packages/piecewiseSEM/ ) dan di GitHub ( https://github.com/jslefche/piecewiseSEM .
