Ringkasan
1. Di sini, saya menyajikan paket filogenetik multifungsi baru, phytools, untuk lingkungan komputasi statistik R.
2. Fokus paket ini adalah pada metode untuk biologi komparatif filogenetik; namun, paket ini juga mencakup alat untuk inferensi pohon, masukan/keluaran filogeni, pembuatan plot, manipulasi, dan beberapa tugas lainnya.
3. Saya menguraikan dan membuat tabulasi metode utama yang diterapkan dalam phytools, dan sebagai tambahan memberikan beberapa demonstrasi penggunaannya dalam bentuk dua contoh ilustrasi.
4. Akhirnya, saya tutup dengan menjelaskan secara singkat web-log aktif yang saya gunakan untuk mendokumentasikan perkembangan phytools saat ini dan di masa mendatang. Saya juga mencatat sumber daya web lain untuk filogenetika dalam lingkungan komputasional R.
Perkenalan
Dalam beberapa dekade terakhir, filogeni telah memegang peranan penting dalam biologi evolusi ( Felsenstein 1985, 2004 ; Harvey & Pagel 1991 ; Losos 2011 ). Di antara para filogenetikus, lingkungan komputasi ilmiah R ( R Development Core Team 2011 ) telah berkembang pesat dalam popularitas, khususnya sejak pengembangan paket R ‘ape’ (Analysis of Phylogenetics and Evolution) multifungsi ( Paradis, Claude & Strimmer 2004 ) dan sejak publikasi buku filogenetik ‘UseR!’ karya Paradis ( Paradis 2006 ). Beberapa tahun terakhir telah menyaksikan perluasan cepat kemampuan filogenetik R dalam bentuk sejumlah paket yang disumbangkan. Sebagian besar, seperti paket populer ‘geiger’ ( Harmon et al. 2008 ) dan ‘phangorn’ ( Schliep 2011 ), bekerja dengan membangun fungsionalitas dan struktur data yang dikembangkan di ape.
Dalam catatan ini, saya akan menjelaskan paket filogenetik baru yang ditulis dalam bahasa R. Pustaka ini disebut ‘phytools’ (alat filogenetik untuk biologi komparatif – dan hal-hal lainnya) dan dapat diinstal dari Comprehensive R Archive Network, CRAN. Dalam paket ini, saya berfokus terutama pada penerapan beberapa metode komparatif filogenetik dari pekerjaan saya sendiri ( Revell 2008, 2009, 2010 ; Revell, Harmon & Collar 2008 ; Revell & Harrison 2008 ; Revell & Collar 2009 ; Lindenfors, Revell & Nunn 2010 ; Mahler et al. 2010 ; Revell et al. in press ); Namun, saya juga telah menyertakan beberapa fungsi baru yang menarik dan berguna bagi komunitas filogenetik yang sebelumnya tidak diimplementasikan dalam R (misalnya Cavalli-Sforza & Edwards 1967 ; Baum 1992 ; Ragan 1992 ; Nielsen 2002 ; Huelsenbeck, Nielsen & Bollback 2003 ; Bollback 2006 ; O’Meara et al. 2006 ; Ives, Midford & Garland 2007 ; Sidlauskas 2008 ), serta sejumlah fungsi utilitas sederhana untuk membaca, menulis, memplot, dan memanipulasi tipe khusus pohon filogenetik.
Selalu, saya telah berusaha untuk memaksimalkan interaktivitas phytools dengan paket ape. Misalnya, salah satu fungsi baru phytools adalah kapasitas untuk menghasilkan, memetakan, membaca, dan menulis pohon karakter yang dipetakan secara stokastik ( Nielsen 2002 ). Daripada membuat tipe objek R baru untuk menyimpan filogeni yang dipetakan secara stokastik, saya malah membangun langsung pada struktur ‘phylo’ yang sudah ada yang dikembangkan untuk ape dan digunakan dalam banyak paket filogenetik R lainnya. Saat ini, phytools tidak dapat dioperasikan dengan paket ‘phylobase’ ( R Hackathon et al. 2011 ), meskipun kemampuan ini akan ditambahkan di masa mendatang.
Pada bagian berikut, saya akan menguraikan fungsionalitas utama pustaka phytools; saya akan memberikan dua contoh ilustrasi yang menunjukkan beberapa fungsionalitas phytools; dan, akhirnya, karena phytools masih dalam tahap pengembangan, saya akan menguraikan web-log yang akan saya gunakan untuk memberikan informasi terkini kepada pengguna phytools tentang bug, pembaruan, dan pengembangan perangkat lunak mendatang untuk paket tersebut.
Keterangan
Pustaka phytools ditulis sepenuhnya dalam bahasa komputasi ilmiah, R ( Tim Inti Pengembangan R 2011 ). Pustaka ini memanfaatkan fungsionalitas yang dikembangkan dalam paket lain, khususnya paket filogenetik inti ape ( Paradis, Claude & Strimmer 2004 ), untuk banyak jenis masukan dan manipulasi pohon filogenetik. Pustaka ini juga menggunakan paket inferensi filogenetik phangorn ( Schliep 2011 ) untuk inferensi dan kalkulasi tertentu lainnya. Selain itu, paket phytools bergantung, mengimpor, atau menyarankan beberapa pustaka R lainnya baik secara langsung, atau melalui dependensinya. Ini termasuk paket-paket berikut: animation: Xie (2011) ; calibrate: Graffelman (2010) ; igraph: Csardi & Nepusz (2006) ; mnormt: Genz & Azzalini (2011) ; msm: Jackson (2011) ; numDeriv: Gilbert (2011) ; quadprog: Turlach & Weingessel (2010) .
Sejauh ini, saya telah menerapkan banyak fungsi untuk paket phytools; namun, saya juga harus mencatat bahwa phytools masih dalam tahap pengembangan dan saya berharap kemampuan phytools akan berkembang pesat dalam beberapa tahun mendatang. Dalam Tabel 1 , saya memberikan daftar beranotasi fungsi-fungsi utama yang sejauh ini telah diterapkan dalam pustaka phytools. Fungsi-fungsi ini mencakup metode-metode dalam beberapa area biologi filogenetik yang berbeda, yang akan dijelaskan kemudian.
Tabel 1. Fungsi utama paket phytools
Nama fungsi Keterangan
tambahkan.dimana-mana Menambahkan ujung ke semua sisi pohon
semuaFurcTrees Menghasilkan semua kemungkinan pohon bercabang dua dan bercabang banyak untuk sekumpulan taksa
tren anc Melakukan estimasi karakter leluhur dengan tren menggunakan kemungkinan
percabangan.difusi Membuat animasi evolusi gerak Brown dengan spesiasi
brownies ringan Menyesuaikan model evolusi Brownian dengan beberapa tingkat menggunakan kemungkinan ( O’Meara et al. 2006 )
jatuhkan.clade Menghapus klade tertentu dari pohon
Keanekaragaman hayati Memperkirakan kepadatan garis keturunan di setiap simpul pohon berdasarkan model ( Mahler et al. 2010 )
laju evolusi.mcmc Menentukan posisi pergeseran laju evolusi menggunakan Bayesian MCMC ( Revell et al. in press )
evolusi.vcv Menyesuaikan beberapa matriks varians-kovarians evolusioner ke pohon menggunakan kemungkinan ( Revell & Collar 2009 )
lengkapMP Melakukan inferensi parsimoni maksimum yang lengkap dan cabang & batas
cepatBM Melakukan simulasi gerak Brown secara cepat menggunakan beberapa model (standar, dengan tren, dengan batas)
fitModel Keragaman Sesuai dengan model evolusi fenotipik yang bergantung pada keanekaragaman ( Mahler et al. 2010 )
uji gamma Melakukan uji γ Pybus & Harvey (2000)
ls.pohon Menghitung panjang cabang kuadrat terkecil untuk topologi pohon dan matriks jarak ( Cavalli-Sforza & Edwards 1967 )
ltt Menciptakan plot garis keturunan lintas waktu, dengan cabang yang punah
buat.era.peta Memetakan interval waktu pada pohon filogenetik
membuat.simmap Menghasilkan peta karakter stokastik untuk data karakter diskrit dan model evolusi ( Nielsen 2002 ; Huelsenbeck, Nielsen & Bollback 2003 )
peta tumpang tindih Menghitung kesamaan dua riwayat karakter yang berbeda
mrp.pohon super Memperkirakan representasi matriks supertree parsimoni dari sekumpulan filogeni ( Baum 1992 ; Ragan 1992 ; Bininda-Emonds 2004 )
optim.phylo.ls Melakukan inferensi filogeni di bawah kriteria kuadrat terkecil ( Cavalli-Sforza & Edwards 1967 ; Felsenstein 2004 )
tempel.pohon Menempelkan dua pohon bersama-sama
fil.cca Melakukan analisis korelasi kanonik filogenetik ( Revell & Harrison 2008 ).
uji berpasangan filum Melakukan uji- t berpasangan filogenetik ( Lindenfors, Revell & Nunn 2010 ).
fil.pca Melakukan analisis komponen utama filogenetik ( Revell 2009 )
fil.residen Melakukan koreksi ukuran filogenetik, menggunakan regresi kuadrat terkecil ( Revell 2009 )
filum RMA Melakukan regresi sumbu utama tereduksi filogenetik
Analisis filogenetik Melakukan anova filogenetik ( Garland et al. 1993 ) dengan perbandingan posthoc rata-rata kelompok
ruang filomorfospasial Memproyeksikan pohon filogenetik ke dalam morfospace bivariat ( Sidlauskas 2008 ; misalnya Gambar 1 ).
filosig Menghitung sinyal filogenetik menggunakan dua metode berbeda ( Pagel 1999 ; Freckleton, Harvey & Pagel 2002 ; Blomberg, Garland & Ives 2003 ) dan menggabungkan kesalahan pengambilan sampel ( Ives, Midford & Garland 2007 )
plotSimmap Membuat peta karakter stokastik dalam bentuk pohon ( Gbr. 3 )
plotpohon Membuat plot pohon filogenetik dengan beberapa opsi ( Gambar 2 )
baca.simmap Membaca satu atau beberapa pohon format peta karakter stokastik dari file ( Bollback 2006 )
susun ulangSimmap Menata ulang tepi pohon format peta stokastik
mengakar ulang Menumbuhkan kembali pohon filogenetik pada posisi sembarang di sepanjang tepian
sim.sejarah Mensimulasikan sejarah stokastik untuk sifat karakter yang dinilai secara diskrit di pohon
tarif sim Mensimulasikan beberapa tingkat evolusi pada pohon menggunakan model evolusi Brown
irisan pohon Memotong pohon dan mengembalikan semua sub pohon
tulis.simmap Fungsi menulis pohon gaya peta stokastik ke file
Biologi Perbandingan
Beberapa metode dalam biologi perbandingan filogenetik telah diterapkan dalam phytools. Metode-metode ini mencakup berbagai bidang termasuk estimasi karakter leluhur (misalnya anc.trend ), metode berbasis kemungkinan untuk mempelajari evolusi sifat karakter dari waktu ke waktu (misalnya brownie.lite , evol.vcv , fitDiversityModel , dan phylosig ), metode Bayesian untuk mendeteksi lokasi pergeseran laju di pohon ( evol.rate.mcmc ), estimasi sinyal filogenetik, termasuk dengan kesalahan pengambilan sampel ( phylosig ), dan berbagai metode untuk pengujian hipotesis statistik dalam konteks filogenetik (misalnya phyl.cca , phyl.pairedttest , phyl.pca , dan phyl.resid ).
Simulasi
Beberapa metode simulasi diimplementasikan dalam phytools. Ini termasuk simulasi gerak Brown dalam berbagai kondisi ( fastBM ), simulasi evolusi karakter diskrit ( sim.history ), simulasi peta karakter stokastik ( make.simmap ), dan simulasi berbagai laju evolusi ( sim.rates ), di antara fungsi lainnya ( Tabel 1 ).
Inferensi Filogenetik
Beberapa prosedur inferensi filogenetik yang berbeda diimplementasikan dalam paket phytools. Fungsi-fungsi ini, secara umum, sangat bergantung pada kalkulasi dan algoritma dalam pustaka phangorn milik Schliep (2011) . Beberapa fungsionalitasnya meliputi estimasi supertree parsimoni representasi matriks ( mrp.supertree ) dan inferensi filogeni kuadrat terkecil ( optim.phylo.ls ; Tabel 1 ).
Metode Grafis
Beberapa metode grafis diimplementasikan dalam phytools. Di antaranya adalah proyeksi pohon ke dalam morfospace bivariat ( phylomorphospace ; Gambar 1 ), pembuatan peta karakter stokastik dan sejarah ( plotSimmap ), pembuatan garis keturunan melalui waktu dengan garis keturunan yang punah ( ltt ), animasi gerak Brown dan spesiasi ( branching.diffusion ), dan fungsi lainnya ( Tabel 1 ).
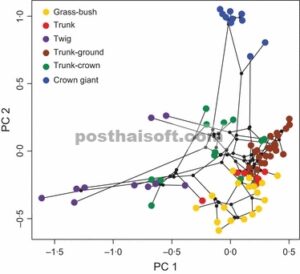
Plot filomorfospasial dari dua sumbu komponen utama yang diperoleh dari data Mahler dkk. (2010) untuk kadal Anolis Karibia . Setiap titik mewakili nilai fenotip spesies (berwarna) atau fenotip leluhur yang dihipotesiskan (hitam). Garis menghubungkan spesies terkait melalui leluhur hipotetis ( Sidlauskas 2008 ). Warna yang berbeda mewakili spesies dalam kategori ekomorfologi yang berbeda yang telah dideskripsikan berdasarkan pemanfaatan mikrohabitat, ekologi, dan kesamaan fenotip kasar ( Losos 2009 ; kode warna ditunjukkan dalam legenda sisipan). Filogeni telah dipangkas untuk hanya menyertakan spesies yang disebut ‘ekomorf’ ini.
Fungsi Utilitas
Selain fungsi ilmiah yang disebutkan di atas, phytools juga mencakup sejumlah fungsi utilitas untuk masukan, keluaran, dan manipulasi filogeni. Fungsi-fungsi ini dimaksudkan untuk melengkapi dan melengkapi berbagai fungsi utilitas yang ada dalam paket kera dan phangorn. Beberapa fungsi ini tercantum dalam Tabel 1 .
Contoh
Untuk menunjukkan penggunaan phytools, saya telah membuat dua contoh ilustrasi singkat yang dapat dengan mudah direproduksi oleh pembaca. Pada contoh pertama, saya menggunakan data simulasi dan fungsi phytools evol.rate.mcmc untuk mengidentifikasi lokasi pergeseran laju evolusi dari waktu ke waktu ( Revell et al. in press ). Pada contoh kedua, saya mensimulasikan riwayat karakter diskrit stokastik dan karakter kontinu dengan laju berbeda yang dikondisikan pada status karakter diskrit, dan kemudian saya menyesuaikan model evolusi karakter Brown multilaju menggunakan fungsi phytools brownie.lite ( O’Meara et al. 2006 ).
Contoh 1: Mendeteksi Lokasi Pergeseran Laju
Dalam contoh ini, saya pertama-tama menyimulasikan filogeni kelahiran-murni yang stokastik; selanjutnya, saya menyimulasikan perubahan evolusi untuk satu karakter bernilai kontinu pada filogeni di bawah dua laju evolusi yang berbeda di berbagai bagian pohon; saya menganalisis pohon dan data menggunakan metode MCMC Bayesian untuk mengidentifikasi lokasi pergeseran laju evolusi seiring berjalannya waktu ( Revell et al. dalam proses penerbitan ); akhirnya, saya menganalisis hasil MCMC untuk memperkirakan lokasi pergeseran dan laju evolusi ke arah ujung dan ke arah akar titik ini.
Pertama, saya memuat paket phytools. Ini juga akan memuat ape dan paket lain yang dibutuhkan pada instansiasi pertama:
> # memuat paket phytools (dan ape)
> memerlukan(phytools)
Memuat paket yang dibutuhkan: phytools
Memuat paket yang diperlukan: ape….
Berikutnya, saya menetapkan benih nomor acak untuk reproduktifitas (di sini, hanya ditetapkan ke 1):
> set.seed(1) # mengatur benih
Saya menggunakan fungsi ape rbdtree untuk mensimulasikan pohon kelahiran murni stokastik. Dalam contoh ini, pohon tersebut memiliki 91 taksa.
> # simulasikan pohon (menggunakan ape)
> tree<-rbdtree(b=log(50),d = 0,Tmax=1) Sekarang, untuk keperluan simulasi, saya membagi pohon pada posisi yang telah ditentukan sebelumnya – yang ditentukan di sini oleh jumlah simpul turunan dan jarak sepanjang tepi dari akar. Untuk melakukan ini, saya menggunakan fungsi phytools splitTree . Perlu dicatat bahwa posisi simpul dan tepi yang digunakan di bawah ini hanya dijamin berfungsi jika dikondisikan pada pengaturan benih nomor acak pada 1 (lihat di atas), jika tidak, titik pembagian yang berbeda harus dipilih. > pohon<-splitTree(pohon,daftar(simpul = 153,bp = 0·09)) Sekarang, saya merentangkan cabang-cabang di satu bagian pohon dan menempelkan kembali sub-pohon untuk simulasi. Untuk menempelkan kembali dua bagian pohon, saya menggunakan fungsi phytools paste.tree sebagai berikut: > # regangkan cabang di satu bagian pohon
> pohon[[2]]$edge.panjang<-pohon[[2]]$edge.panjang*10 > # pasang kembali dua sub pohon
> sim.pohon<-tempel.pohon(pohon[[1]],pohon[[2]])
Saya kemudian dapat memetakan pohon pembangkit untuk simulasi (yang cabang-cabangnya direntangkan agar proporsional terhadap laju evolusi dikalikan waktu; Gambar 2 ), menggunakan fungsi phytools plotTree , dan melakukan simulasi pada pohon yang direntangkan ini menggunakan fungsi phytools fastBM :
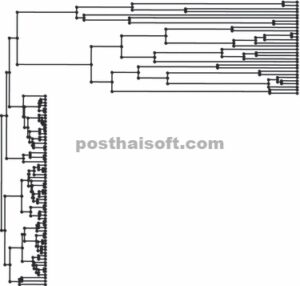
Pohon filogenetik disimulasikan dalam contoh ilustrasi 1. Cabang-cabang pohon telah diskalakan ulang untuk mewakili laju evolusi dikalikan dengan waktu yang berlalu (dengan demikian, cabang yang lebih panjang memiliki laju evolusi yang lebih tinggi).
> # plot pohon pembangkit untuk simulasi
> plotTree(pohon sim,ukuran f = 0·5)
> x<-fastBM(sim.tree) # simulasi di pohon Sekarang, saya melakukan analisis Bayesian MCMC menggunakan fungsi phytools evol.rate.mcmc ( Revell et al. in press ). Analisis ini memerlukan waktu sekitar 20 menit pada CPU Dell i5 650 yang berjalan pada 3·20 GHz. > # melakukan MCMC > res<-evol.rate.mcmc(pohon,x,ngen = 100000) Parameter kontrol (ditetapkan oleh pengguna atau default): Daftar 11 $ sig1 : angka 4·34 $ sig2 : angka 4·34 $ a : nomor 0·0222 $ sd1 : nomor 0·867 $ sd2 : nomor 0·867 $ sda : nomor 0·00444 $ kloc : jumlah 0·2 $ sdlnr : nomor 1 $ rand.shift: angka 0·05 $ cetak : angka 100 $ contoh : num 100 Memulai lari MCMC: negara sig1 sig2 a node bp kemungkinan 04·3352 4·3352 0·0222 35 0·345 − 130·7022 negara sig1 sig2 a node bp kemungkinan 1004·8517 0·9447 − 0·0248 93 0·044 − 116·3554 negara sig1 sig2 a node bp kemungkinan 2006·7915 1·2872 − 0·0205 153 0·057 − 101·0501 …. Selesai menjalankan MCMC. Fungsi MCMC pertama-tama mencetak parameter kontrol (yang dapat diatur oleh pengguna, meskipun di atas telah diberikan nilai default, lihat di bawah), lalu mencetak status rantai MCMC pada frekuensi yang diberikan oleh parameter kontrol print (di sini, setiap 100 generasi; generasi setelah 200 tidak ditampilkan di atas). Selanjutnya, saya dapat memperkirakan lokasi titik pergeseran dengan menemukan pemisahan pada sampel posterior dengan jarak total terkecil ke semua sampel lainnya (ini adalah salah satu dari beberapa kriteria yang mungkin; lihat Revell et al. in press ). Untuk analisis ini, saya menggunakan fungsi phytools minSplit dan mengecualikan 20.000 generasi pertama sebagai burn-in: >est.split<-minSplit(pohon,res$mcmc[201:nrow(res$mcmc),]) Analisis ini memakan waktu sekitar 6 detik untuk dijalankan pada perangkat keras yang sama seperti yang dijelaskan sebelumnya. Akhirnya, saya perlu melakukan praproses sampel posterior untuk mendapatkan laju sampel ke arah ujung dan ke arah akar dari pergeseran rata-rata, untuk setiap sampel (lihat Revell et al. in press ). Saya melakukan ini menggunakan fungsi phytools posterior.evolrate . Saya kemudian dapat mencetak hasilnya (perkiraan titik pergeseran dan laju evolusi) ke layar: > pp.hasil<-posterior.evolrate(pohon,est.split,res$mcmc[201:nrow(res$mcmc),], res$tips[201:nrow(res$mcmc)]) > est.sig1<-rata-rata(pp.hasil[,“sig1”]) > est.sig2 <-rata-rata(pp.hasil[,“sig2”]) > est.terbagi
$simpul
[1] 153
$bp
[1] 0·1003489
> perkiraan tanda tangan1
[1] 1·010709
> perkiraan tanda2
[1] 10·24914
Analisis ini memakan waktu sekitar 9 detik untuk diselesaikan.
Di sini, estimasi parameter sangat dekat dengan titik pergeseran pembangkitan [153, 0·09] dan tingkat evolusi pembangkitan gambar sebarisdan gambar sebaris.
Perlu dicatat bahwa dalam praktik sebenarnya, penulis harus lebih memperhatikan parameter kontrol MCMC daripada yang diberikan di sini, dan khususnya, pada distribusi proposal untuk parameter model. Informasi lebih lanjut tentang kontrol fungsi dapat diperoleh dengan memanggil berkas bantuan evol.rate.mcmc:
> ?evol.rate.mcmc
atau dengan merujuk ke Revell et al. (sedang diterbitkan) . Selain itu, pengguna harus menilai konvergensi dan menghitung ukuran sampel efektif untuk sampel mereka dari distribusi posterior. Ini dapat dilakukan dengan menggunakan paket diagnostik MCMC ‘coda’ ( Plummer et al. 2006 ). Silakan merujuk ke Revell et al. (sedang diterbitkan) untuk informasi lebih lanjut tentang metode ini.
Contoh 2: Simulasikan dan Analisis Evolusi Brown Multi-Laju
Dalam contoh ini, pertama-tama saya simulasikan sejarah karakter dari sifat karakter yang dinilai secara diskret dengan tiga status yang berevolusi pada filogeni. Kemudian saya simulasikan evolusi sifat berkelanjutan dengan laju yang bergantung pada nilai sifat diskret. Terakhir, saya sesuaikan model evolusi laju tunggal dan ganda ke data dan pohon menggunakan metode kemungkinan O’Meara et al. (2006) .
Setelah memuat phytools, pertama-tama saya menetapkan benih (secara acak ke 10; dilakukan di sini hanya untuk reproduktifitas):
> atur.benih(10)
Sekarang, saya mensimulasikan pohon kelahiran murni stokastik menggunakan ape:
> pohon<-rbdtree(b = log(50),d = 0,Tmax = 1) Pohon ini berisi 129 taksa. Selanjutnya, saya mensimulasikan riwayat karakter stokastik pada pohon untuk karakter dengan tiga status, A , B , dan C , menggunakan fungsi phytools sim.history sebagai berikut: > # ini adalah matriks transisi kita
> Q<-matrix(c( − 2,1,1,1, − 2,1,1,1, − 2),3,3) > namabaris(Q)<-namakolom(Q)<-c(“A”,“B”,“C”) > mtree<-sim.history(pohon,Q) Saya dapat memetakan riwayat simulasi menggunakan fungsi phytools plotSimmap untuk melihat seperti apa tampilannya: > # mengatur warna > kolom<-c(“merah”,”biru”,”hijau”); > nama(kolom)<-namabaris(Q) > # plot pohon dengan label mati
> plotSimmap(mtree,cols,ftype=“mati”)
Visualisasi ini ditunjukkan pada Gambar 3 .

Riwayat stokastik yang disimulasikan untuk Contoh 2 yang bersifat ilustratif . Di sini, cabang-cabang dengan warna yang berbeda menunjukkan keadaan simulasi yang berbeda untuk sifat karakter yang bernilai diskret yang berevolusi di pohon. Kode warnanya adalah A: merah, B: biru, dan C: hijau.
Berikutnya, saya melakukan simulasi evolusi karakter berkelanjutan menggunakan tiga tingkat berbeda menggunakan fungsi phytools sim.rates :
> # tetapkan tarif
> sig2 <-c(1,10,100) >nama(sig2)<-namabaris(Q) > X<-sim.rates(mtree,sig2) # simulasi Akhirnya, saya menyesuaikan model Brownian multi-rate menggunakan metode likelihood dari O’Meara et al. (2006) dengan fungsi phytools brownie.lite . Optimasi likelihood ini memakan waktu sekitar 3 detik untuk dijalankan pada perangkat keras yang sama yang dijelaskan sebelumnya. > fit.bm<-brownie.lite(mtree,X,maxit=4000) > cocok.bm
$sig2.tunggal
[1] 47·15693
$satu.tunggal
[1] − 5·242448
$var.tunggal
[1] 34·47709
$logL1
[1] − 329·7582
$k1
[1] 2
$sig2.berganda
BCA
10·4646399 99·9563314 0·8247106
…
$logL.berganda
[1] − 287·4271
$k2
[1] 4
$P.chisq
[1] 4·129091e-19
$konvergensi
[1] “Optimasi telah terkonvergensi.”
Perlu dicatat bahwa urutan tiga rezim laju dalam model yang disesuaikan adalah urutan kemunculannya di pohon ( Gbr. 3 ), bukan dalam urutan abjad atau numerik. Dalam kasus ini, estimasi parameter yang disesuaikan (0·82, 10·46, 99·96) sangat dekat dengan nilai pembangkitannya (1, 10, dan 100). Untuk detail lebih lanjut tentang metode kemungkinan ini, silakan lihat O’Meara et al. (2006) atau Revell (2008) .
blog pengembangan phytools dan sumber daya lainnya
Paket ini sejauh ini mengimplementasikan sejumlah metode untuk biologi komparatif filogenetik, inferensi filogeni, manipulasi pohon, dan grafik. Namun, proyek phytools masih dalam tahap pengerjaan. Untuk terus memberi informasi terkini kepada pengguna phytools tentang bug, perbaikan, dan fungsi baru, saya mengelola web-log aktif (yaitu ‘blog’; http://phytools.blogspot.com ). Blog ini bertindak sebagai penghubung antara pengembang (saat ini saya sendiri) dan pengguna paket phytools, serta semacam buku catatan lab terbuka ( Butler 2005 ; Bradley et al. 2011 ) tempat saya mendokumentasikan detail perbaikan bug, implementasi perangkat lunak, dan penggunaan. Sebagian besar fungsi yang tercantum sebelumnya telah ditampilkan di blog (dalam proses pengembangan dan penyempurnaan). Pekerjaan selanjutnya pada phytools juga akan didokumentasikan di sini.
Terakhir, selain blog saya, ada sejumlah forum web dan email bermanfaat lainnya untuk phytools dan filogenetik dalam bahasa R secara umum. CRAN Task View filogenetik ( http://cran.r-project.org/web/views/Phylogenetics.html ) dan milis email R-sig-phylo ( https://stat.ethz.ch/mailman/listinfo/r-sig-phylo ) adalah dua sumber daya terpenting tersebut.
Kutipan phytools
Ilmuwan yang menggunakan phytools dalam makalah yang diterbitkan harus mengutip artikel ini. Pengguna juga dapat mengutip paket phytools secara langsung jika mereka menginginkannya. Informasi kutipan dapat diperoleh dengan mengetik:
> kutipan(“phytools”)
pada prompt perintah.
Ucapan Terima Kasih
Penghargaan diberikan kepada L. Harmon karena telah mendorong saya untuk mempelajari R, mengembangkan phytools, dan menerbitkan catatan ini. Terima kasih kepada L. Mahler karena telah membagikan datanya dan membantu membuat Gambar 2. C. Boettiger, seorang editor asosiasi, dan seorang pengulas anonim memberikan kritik yang sangat membantu pada versi awal artikel ini.
