Ringkasan
Penggunaan model efek campuran linier dan linier umum (LMM dan GLMM) telah menjadi populer tidak hanya dalam ilmu sosial dan kedokteran, tetapi juga dalam ilmu biologi, terutama di bidang ekologi dan evolusi. Kriteria informasi, seperti Kriteria Informasi Akaike (AIC), biasanya disajikan sebagai alat perbandingan model untuk model efek campuran.
Namun, penyajian ‘varians yang dijelaskan’ ( R 2 ) sebagai statistik ringkasan yang relevan dari model efek campuran jarang dilakukan, meskipun R 2 secara rutin dilaporkan untuk model linier (LM) dan juga model linier umum (GLM). R 2 memiliki sifat yang sangat berguna dalam memberikan nilai absolut untuk kebaikan-kesesuaian model, yang tidak dapat diberikan oleh kriteria informasi. Sebagai statistik ringkasan yang menggambarkan jumlah varians yang dijelaskan, R 2 juga dapat menjadi kuantitas yang menarik secara biologis.
Salah satu alasan kurangnya apresiasi R 2 untuk model efek campuran terletak pada fakta bahwa R 2 dapat didefinisikan dalam sejumlah cara. Lebih jauh, sebagian besar definisi R 2 untuk efek campuran memiliki masalah teoritis (misalnya nilai R 2 yang menurun atau negatif dalam model yang lebih besar) dan/atau penggunaannya terhalang oleh kesulitan praktis (misalnya implementasi).
Di sini, kami memaparkan pentingnya pelaporan R 2 untuk model efek campuran. Pertama-tama kami memberikan definisi umum R 2 untuk LM dan GLM dan membahas masalah utama yang terkait dengan penghitungan R 2 untuk model efek campuran. Kemudian kami merekomendasikan metode umum dan sederhana untuk menghitung dua jenis R 2 ( R 2 marginal dan kondisional ) untuk LMM dan GLMM, yang kurang rentan terhadap masalah umum.
Metode ini diilustrasikan dengan contoh-contoh dan dapat digunakan secara luas oleh para peneliti di bidang penelitian apa pun, terlepas dari paket perangkat lunak yang digunakan untuk menyesuaikan model efek campuran. Metode yang diusulkan memiliki potensi untuk memfasilitasi penyajian R 2 untuk berbagai keadaan.
Perkenalan
Banyak set data biologi memiliki beberapa strata karena sifat hierarkis dunia biologi, misalnya, sel dalam individu, individu dalam populasi, populasi dalam spesies dan spesies dalam komunitas. Oleh karena itu, kita memerlukan metode statistik yang secara eksplisit memodelkan struktur hierarkis data nyata. Model efek campuran linier (LMM; juga disebut sebagai model multilevel/hierarkis) dan perluasannya, model efek campuran linier umum (GLMM) membentuk kelas model yang menggabungkan hierarki multilevel dalam data. Memang, LMM dan GLMM menjadi bagian dari perangkat metodologi standar dalam ilmu biologi (Bolker et al . 2009 ), serta dalam ilmu sosial dan medis (Gelman & Hill 2007 ; Congdon 2010 ; Snijders & Bosker 2011 ). Penggunaan GLMM secara luas menunjukkan bahwa statistik yang merangkum kebaikan-kesesuaian model efek campuran dengan data akan menjadi sangat penting. Tampaknya saat ini tidak ada statistik ringkasan yang diterima secara luas untuk model efek campuran.
Banyak ilmuwan secara tradisional telah menggunakan koefisien determinasi, R2 ( berkisar dari 0 hingga 1), sebagai statistik ringkasan untuk mengukur kesesuaian model efek tetap seperti regresi linier berganda, anova , ancova, dan model linier umum (GLM). Konsep R2 sebagai ‘varians yang dijelaskan’ bersifat intuitif. Karena R2 tidak memiliki satuan, konsep ini sangat berguna sebagai indeks ringkasan untuk model statistik karena seseorang dapat mengevaluasi kesesuaian model secara objektif dan membandingkan nilai R2 di seluruh studi dengan cara yang sama seperti statistik ukuran efek standar dalam beberapa keadaan ( misalnya model dengan respons yang sama dan serangkaian prediktor yang sama atau dengan kata lain, konsep ini dapat digunakan untuk meta-analisis; Nakagawa & Cuthill 2007 ).
Dalam Tabel 1 , kami meringkas secara singkat 12 properti R 2 (berdasarkan Kvålseth 1985 dan Cameron & Windmeijer 1996 ; kompilasi diadopsi dari Orelien & Edwards 2008 ) yang akan memberikan pembaca dengan rasa yang baik tentang apa yang seharusnya menjadi statistik R 2 ‘tradisional’ dan juga memberikan tolok ukur untuk menggeneralisasi R 2 ke model efek campuran. Menggeneralisasi R 2 dari model linear (LM) ke LMM dan GLMM ternyata menjadi tugas yang sulit. Sejumlah cara untuk memperoleh R 2 untuk model campuran telah diusulkan (misalnya Snijders & Bosker 1994 ; Xu 2003 ; Liu, Zheng & Shen 2008 ; Orelien & Edwards 2008 ). Namun, metode yang diusulkan ini memiliki beberapa masalah teoritis atau kesulitan praktis (dibahas secara rinci di bawah), dan akibatnya, tidak ada konsensus untuk definisi R 2 untuk model efek campuran yang muncul dalam literatur statistik. Oleh karena itu, tidak mengherankan bahwa R 2 jarang dilaporkan sebagai statistik ringkasan model ketika model campuran digunakan.
Tabel 1. Dua belas properti R 2 ‘tradisional’ untuk model regresi; diadopsi dari Orelien & Edwards ( 2008 )
Milik Referensi
R 2 harus mewakili kebaikan kecocokan dan memiliki interpretasi yang intuitif Kvålseth ( 1985 )
R 2 harus bebas satuan; yaitu, tidak berdimensi Kvålseth ( 1985 )
R 2 harus berkisar dari 0 hingga 1 di mana 1 mewakili kesesuaian yang sempurna Kvålseth ( 1985 )
R 2 harus cukup umum untuk diterapkan pada semua jenis model statistik Kvålseth ( 1985 )
Nilai R 2 tidak boleh dipengaruhi oleh teknik pemasangan model yang berbeda Kvålseth ( 1985 )
Nilai R2 dari model yang berbeda yang dipasang pada data yang sama harus dapat dibandingkan secara langsung Kvålseth ( 1985 )
Nilai R2 relatif harus sebanding dengan ukuran kesesuaian yang diterima lainnya Kvålseth ( 1985 )
Semua residual (positif dan negatif) harus diberi bobot yang sama dengan R 2 Kvålseth ( 1985 )
Nilai R2 harus selalu meningkat seiring dengan penambahan prediktor (tanpa koreksi derajat kebebasan ) Cameron dan Windmeijer ( 1996 )
Nilai R2 berdasarkan jumlah kuadrat residual dan nilai yang berdasarkan jumlah kuadrat yang dijelaskan harus sesuai Cameron dan Windmeijer ( 1996 )
Nilai R2 dan signifikansi statistik parameter kemiringan harus menunjukkan korespondensi Cameron dan Windmeijer ( 1996 )
R 2 harus dapat diinterpretasikan dalam konteks konten informasi data Cameron dan Windmeijer ( 1996 )
Jika tidak ada R 2 , kriteria informasi sering digunakan dan dilaporkan sebagai alat perbandingan untuk model campuran. Kriteria informasi didasarkan pada kemungkinan data yang diberikan model yang disesuaikan (‘kemungkinan’) yang dihukum oleh jumlah parameter model yang diestimasikan. Kriteria informasi yang umum digunakan meliputi Kriteria Informasi Akaike (AIC) (Akaike 1973 ), kriteria informasi Bayesian (BIC), (Schwarz 1978 ) dan kriteria informasi deviasi (DIC) yang diusulkan baru-baru ini, (Spiegelhalter et al . 2002 ; diulas dalam Claeskens & Hjort 2009 ; Grueber et al . 2011 ; Hamaker et al . 2011 ). Kriteria informasi digunakan untuk memilih model ‘terbaik’ atau ‘lebih baik’, dan memang berguna untuk memilih model yang paling parsimonius dari set model kandidat (Burnham & Anderson 2002 ). Akan tetapi, setidaknya ada tiga batasan penting dalam penggunaan kriteria informasi dalam kaitannya dengan R2 : (i) meskipun kriteria informasi memberikan estimasi kecocokan relatif model-model alternatif, kriteria tersebut tidak memberi tahu kita apa pun tentang kecocokan model absolut (lih. rasio bukti; Burnham & Anderson 2002 ) , (ii) kriteria informasi tidak memberikan informasi apa pun tentang varians yang dijelaskan oleh model (Orelien & Edwards 2008 ), dan (iii) kriteria informasi tidak dapat dibandingkan di seluruh kumpulan data yang berbeda dalam keadaan apa pun, karena kriteria tersebut sangat spesifik terhadap kumpulan data (dengan kata lain, kriteria tersebut bukanlah statistik efek terstandarisasi yang dapat digunakan untuk meta-analisis; Nakagawa & Cuthill 2007 ).
Dalam makalah ini, kami mulai dengan memberikan definisi R 2 yang paling umum dalam LM dan GLM. Kami kemudian meninjau definisi pengukuran R 2 yang diusulkan sebelumnya untuk model efek campuran dan membahas masalah dan kesulitan yang terkait dengan pengukuran ini. Terakhir, kami menjelaskan metode umum dan sederhana untuk menghitung varians yang dijelaskan oleh LMM dan GLMM dan mengilustrasikan penggunaannya dengan kumpulan data ekologi yang disimulasikan.
Definisi R 2
Pada bagian ini, pertama-tama kami akan menjelaskan beberapa metode yang ada untuk memperkirakan koefisien determinasi, R 2 , untuk LM. Model linier (umum) standar (LM) dapat ditulis sebagai:
guci:x-wiley:2041210X:media:mee3261:mee3261-matematika-0001
(persamaan 1)
guci:x-wiley:2041210X:media:mee3261:mee3261-matematika-0002
(persamaan 2)
di mana yi adalah nilai respons ke – i, x hi adalah nilai ke – i untuk prediktor ke -h , β0 adalah intersep, βh adalah kemiringan (koefisien regresi) dari prediktor ke- h , hi adalah nilai residu ke- i dan kesalahan residu terdistribusi normal (Gaussian) dengan varians . Model regresi tersebut dipasang dengan metode kuadrat terkecil biasa (OLS) yang meminimalkan jumlah jarak kuadrat antara respons yang diamati dan yang dipasang (yaitu meminimalkan jumlah kuadrat residual). Jumlah kuadrat residual muncul dalam formulasi definisi yang paling umum untuk koefisien determinasi, R2 ( Kvålseth 1985 ; Draper & Smith 1998 ). guci:x-wiley:2041210X:media:mee3261:mee3261-matematika-0003
guci:x-wiley:2041210X:media:mee3261:mee3261-matematika-0004
(persamaan 3)
guci:x-wiley:2041210X:media:mee3261:mee3261-matematika-0005
(persamaan 4)
di mana n adalah jumlah observasi (yaitu ukuran sampel total), guci:x-wiley:2041210X:media:mee3261:mee3261-matematika-0006adalah rata-rata respons, guci:x-wiley:2041210X:media:mee3261:mee3261-matematika-0007adalah nilai respons yang disesuaikan ke-i, adalahguci:x-wiley:2041210X:media:mee3261:mee3261-matematika-0008 estimasi β 0 dan β h , masing-masing, dan subskrip ‘O’ dalam R 2 O menandakan regresi OLS. Fitur yang menarik dan penting untuk dicatat di sini adalah bahwa definisi ‘varians yang dijelaskan’ secara tidak langsung terdiri dari 1 dikurangi ‘varians yang tidak dijelaskan’ (kita akan membahas kembali poin ini nanti). Rumusan yang setara namun mungkin lebih intuitif dari guci:x-wiley:2041210X:media:mee3261:mee3261-matematika-0009juga dapat ditulis sebagai:
guci:x-wiley:2041210X:media:mee3261:mee3261-matematika-0010
(persamaan 5)
guci:x-wiley:2041210X:media:mee3261:mee3261-matematika-0011
(persamaan 6)
di mana ‘var’ menunjukkan varians dari apa yang ada dalam tanda kurung berikut. Persamaan 6 juga dapat dinyatakan sebagai rasio antara varians residual dari model yang diinginkan dan varians residual dari model nol (juga disebut sebagai model kosong atau model intersep):
guci:x-wiley:2041210X:media:mee3261:mee3261-matematika-0012
(persamaan 7)
di mana guci:x-wiley:2041210X:media:mee3261:mee3261-matematika-0013merupakan varians residual dari model nol.
Ada dua kesulitan dalam menggeneralisasi definisi ini guci:x-wiley:2041210X:media:mee3261:mee3261-matematika-0014ke dalam konteks GLMM. Ketika menggeneralisasi ke variabel respons non-Gaussian (yaitu GLM), tidak mudah untuk mendapatkan estimasi varians residual yang tepat. Selain itu, ketika menggeneralisasi ke model efek campuran yang terdiri dari istilah galat pada tingkat hierarki yang berbeda (lihat di bawah), tidak langsung jelas estimasi mana yang harus digunakan sebagai varians yang tidak dapat dijelaskan. Untuk GLM, guci:x-wiley:2041210X:media:mee3261:mee3261-matematika-0015dapat didefinisikan menggunakan kemungkinan maksimum (ML) dari model penuh dan nol (Maddala 1983 ). Mungkin, definisi yang paling terkenal dan paling populer adalah:
guci:x-wiley:2041210X:media:mee3261:mee3261-matematika-0016
(persamaan 8)
di mana L β adalah kemungkinan data yang diberikan model minat yang sesuai dan L 0 adalah kemungkinan data yang diberikan model nol, n adalah ukuran sampel total, subskrip ‘g’ dalam guci:x-wiley:2041210X:media:mee3261:mee3261-matematika-0017menandakan ‘umum’ (formulasi ini didasarkan pada peningkatan kuadrat rata-rata geometris; lihat Menard 2000 ). Karena guci:x-wiley:2041210X:media:mee3261:mee3261-matematika-0018tidak dapat menjadi 1 bahkan ketika model minat sesuai dengan data dengan sempurna, Nagelkerke ( 1991 ) mengusulkan penyesuaian pada Persamaan eqn 8 :
guci:x-wiley:2041210X:media:mee3261:mee3261-matematika-0019
(persamaan 9)
di mana suku penyebut dapat diartikan sebagai nilai maksimum yang mungkin dari guci:x-wiley:2041210X:media:mee3261:mee3261-matematika-0020dan subskrip ‘G’ di dalam guci:x-wiley:2041210X:media:mee3261:mee3261-matematika-0021menandakan ‘Umum’. Definisi R 2 , yang sebanding dengan guci:x-wiley:2041210X:media:mee3261:mee3261-matematika-0022, adalah:
guci:x-wiley:2041210X:media:mee3261:mee3261-matematika-0023
(persamaan 10)
Kami sengaja meninggalkan −2 di penyebut dan pembilang sehingga guci:x-wiley:2041210X:media:mee3261:mee3261-matematika-0024(‘D’ menandakan ‘deviasi’) dapat dibandingkan dengan Persamaan persamaan 3. Untuk LM (Persamaan persamaan 1 ), statistik log-likelihood −2 (kadang-kadang disebut deviasi) sama dengan jumlah kuadrat residual berdasarkan OLS model ini (Menard 2000 ; lihat serangkaian guci:x-wiley:2041210X:media:mee3261:mee3261-matematika-0025rumus untuk respons non-Gaussian di Tabel 1 dari Cameron & Windmeijer 1997 ). Ada beberapa definisi berbasis kemungkinan lain dari R2 ( diulas dalam Cameron & Windmeijer 1997 ; Menard 2000 ), tetapi kami tidak mengulas definisi ini, karena kurang relevan dengan pendekatan kami di bawah ini. Sebagai gantinya , kami akan membahas generalisasi R2 ke LMM dan GLMM, dan masalah terkait dalam proses ini, di bagian berikutnya.
Masalah umum saat menggeneralisasi R 2
Pertama, mari kita bayangkan sebuah desain eksperimen di mana kita mengambil sampel berulang kali dari kumpulan individu yang sama. Dengan memperluas LM yang ditunjukkan dalam Persamaan 1-persamaan 2 , kita dapat menyesuaikan LMM dengan satu faktor acak (‘individu’ dalam contoh kita) yang didefinisikan sebagai:
guci:x-wiley:2041210X:media:mee3261:mee3261-matematika-0026
(persamaan 11)
guci:x-wiley:2041210X:media:mee3261:mee3261-matematika-0027
(persamaan 12)
guci:x-wiley:2041210X:media:mee3261:mee3261-matematika-0028
(persamaan 13)
di mana y ij adalah respons ke – i dari individu ke- j , x hij adalah nilai ke – i dari individu ke -j untuk prediktor ke -h , β 0 adalah intersep, β h adalah kemiringan (koefisien regresi) dari prediktor ke-h , α j adalah efek khusus individu dari distribusi normal efek khusus individu dengan rata-rata nol dan varians guci:x-wiley:2041210X:media:mee3261:mee3261-matematika-0029(varians antar-individu) dan εegr; ij adalah residual yang terkait dengan nilai ke – i dari individu ke -j dari distribusi normal residual dengan rata-rata nol dan varians guci:x-wiley:2041210X:media:mee3261:mee3261-matematika-0030(varians dalam-individu). Seperti yang terlihat pada persamaan sebelumnya, LMM menurut definisi memiliki lebih dari satu komponen varians (dalam kasus ini dua: guci:x-wiley:2041210X:media:mee3261:mee3261-matematika-0031dan guci:x-wiley:2041210X:media:mee3261:mee3261-matematika-0032), sementara LM hanya memiliki satu (Persamaan eqn 1 dan eqn 2 ).
Salah satu definisi paling awal R 2 untuk model efek-campuran didasarkan pada pengurangan masing-masing komponen varians ketika memasukkan prediktor efek-tetap secara terpisah; dengan kata lain, pisahkan R 2 untuk masing-masing efek acak dan varians residual (Raudenbush & Bryk 1986 ; Bryk & Raudenbush 1992 ; kami merinci pengukuran ini di bagian ‘Masalah terkait’). Pendekatan ini analog dengan Persamaan eqn 7 . Namun, seperti yang ditunjukkan oleh Snijders & Bosker ( 1994 ), tidaklah jarang bahwa beberapa prediktor dapat mengurangi guci:x-wiley:2041210X:media:mee3261:mee3261-matematika-0033sementara secara bersamaan meningkatkan guci:x-wiley:2041210X:media:mee3261:mee3261-matematika-0034, dan sebaliknya meskipun jumlah total komponen varians guci:x-wiley:2041210X:media:mee3261:mee3261-matematika-0035biasanya berkurang (untuk contoh, lihat Tabel 1 di Snijders & Bosker 1994 ). Perilaku komponen varians seperti itu kadang-kadang dapat menghasilkan R 2 negatif karena guci:x-wiley:2041210X:media:mee3261:mee3261-matematika-0036dan guci:x-wiley:2041210X:media:mee3261:mee3261-matematika-0037dapat lebih besar dari guci:x-wiley:2041210X:media:mee3261:mee3261-matematika-0038dan guci:x-wiley:2041210X:media:mee3261:mee3261-matematika-0039, masing-masing (yaitu komponen varians yang sesuai dalam model intersep).
Untuk menghindari masalah ini, Snijders & Bosker ( 1994 ) mengusulkan apa yang mereka sebut sebagai guci:x-wiley:2041210X:media:mee3261:mee3261-matematika-0040dan guci:x-wiley:2041210X:media:mee3261:mee3261-matematika-0041untuk LMM dengan satu faktor acak (seperti pada Persamaan persamaan 11 ): satu nilai R 2 dihitung untuk setiap level LMM (yaitu level unit dan level pengelompokan/individu). guci:x-wiley:2041210X:media:mee3261:mee3261-matematika-0042dapat dinyatakan dalam dua bentuk (analog dengan Persamaan persamaan 5 dan persamaan 7 ):
guci:x-wiley:2041210X:media:mee3261:mee3261-matematika-0043
(persamaan 14)
guci:x-wiley:2041210X:media:mee3261:mee3261-matematika-0044
(persamaan 15)
guci:x-wiley:2041210X:media:mee3261:mee3261-matematika-0045
(persamaan 16)
di mana guci:x-wiley:2041210X:media:mee3261:mee3261-matematika-0046adalah varians yang dijelaskan pada unit analisis (yaitu level 1; varians dalam individu yang dijelaskan), guci:x-wiley:2041210X:media:mee3261:mee3261-matematika-0047adalah nilai yang disesuaikan ke – i untuk individu ke-j dan notasi lainnya seperti di atas. Dengan cara yang sama, guci:x-wiley:2041210X:media:mee3261:mee3261-matematika-0048dapat ditulis sebagai:
guci:x-wiley:2041210X:media:mee3261:mee3261-matematika-0049
(persamaan 17)
guci:x-wiley:2041210X:media:mee3261:mee3261-matematika-0050
(persamaan 18)
guci:x-wiley:2041210X:media:mee3261:mee3261-matematika-0051
(persamaan 19)
di mana guci:x-wiley:2041210X:media:mee3261:mee3261-matematika-0052adalah varians yang dijelaskan pada tingkat individu (yaitu tingkat 2; varians antar-individu yang dijelaskan), guci:x-wiley:2041210X:media:mee3261:mee3261-matematika-0053adalah nilai rata-rata yang diamati untuk individu ke- j , guci:x-wiley:2041210X:media:mee3261:mee3261-matematika-0054adalah nilai yang disesuaikan untuk individu ke -j , k adalah rata-rata harmonik dari jumlah replikasi per individu, m j adalah jumlah replikasi untuk individu ke -i , M adalah jumlah total individu, dan notasi lainnya seperti di atas. Keuntungan menggunakan guci:x-wiley:2041210X:media:mee3261:mee3261-matematika-0055dan guci:x-wiley:2041210X:media:mee3261:mee3261-matematika-0056adalah kita dapat mengevaluasi seberapa banyak varians yang dijelaskan pada setiap tingkat analisis. Namun, setidaknya ada tiga masalah dengan pendekatan ini: (i) ternyata guci:x-wiley:2041210X:media:mee3261:mee3261-matematika-0057dan guci:x-wiley:2041210X:media:mee3261:mee3261-matematika-0058dapat berkurang dalam model yang lebih besar (perhatikan bahwa guci:x-wiley:2041210X:media:mee3261:mee3261-matematika-0059hanya dapat meningkat ketika lebih banyak prediktor ditambahkan tanpa penyesuaian derajat kebebasan; lihat Tabel 1 ), (ii) tidak jelas bagaimana guci:x-wiley:2041210X:media:mee3261:mee3261-matematika-0060dan guci:x-wiley:2041210X:media:mee3261:mee3261-matematika-0061dapat diperluas ke lebih dari dua tingkat (yaitu lebih dari satu faktor acak) dan (iii) juga tidak jelas bagaimana guci:x-wiley:2041210X:media:mee3261:mee3261-matematika-0062dan guci:x-wiley:2041210X:media:mee3261:mee3261-matematika-0063harus digeneralisasi ke GLMM.
Masalah pertama berarti bahwa karena ( guci:x-wiley:2041210X:media:mee3261:mee3261-matematika-0064) dari model dengan lebih banyak prediktor dapat lebih besar daripada model dengan lebih sedikit prediktor, guci:x-wiley:2041210X:media:mee3261:mee3261-matematika-0065dan guci:x-wiley:2041210X:media:mee3261:mee3261-matematika-0066juga dapat mengambil nilai negatif (Snijders & Bosker 1994 ). Dengan kata lain, estimasi dari guci:x-wiley:2041210X:media:mee3261:mee3261-matematika-0067dapat lebih besar daripada ( guci:x-wiley:2041210X:media:mee3261:mee3261-matematika-0068). Snijders & Bosker ( 1999 ) menawarkan dua penjelasan untuk penurunan R 2 dan/atau R 2 negatif dalam model yang lebih besar: (i) fluktuasi peluang (atau varians sampling) yang paling menonjol ketika ukuran sampel kecil atau (ii) kesalahan spesifikasi model, ketika prediktor baru tersebut redundan dalam kaitannya dengan satu atau lebih prediktor lain dalam model. Snijders & Bosker ( 1999 ) menyarankan bahwa penurunan dalam guci:x-wiley:2041210X:media:mee3261:mee3261-matematika-0069dan guci:x-wiley:2041210X:media:mee3261:mee3261-matematika-0070(perubahan dalam arah yang ‘salah’) dapat digunakan sebagai diagnostik dalam pemilihan model. Namun, kesalahan spesifikasi tersebut tidak perlu menjadi penyebab peningkatan dalam ( guci:x-wiley:2041210X:media:mee3261:mee3261-matematika-0071) (dan akibatnya penurunan dalam guci:x-wiley:2041210X:media:mee3261:mee3261-matematika-0072dan guci:x-wiley:2041210X:media:mee3261:mee3261-matematika-0073).
Masalah kedua dalam memperluas guci:x-wiley:2041210X:media:mee3261:mee3261-matematika-0074dan guci:x-wiley:2041210X:media:mee3261:mee3261-matematika-0075ke model dengan lebih dari dua level telah diatasi oleh Gelman & Pardoe ( 2006 ), yang memberikan solusi untuk memperluas guci:x-wiley:2041210X:media:mee3261:mee3261-matematika-0076dan guci:x-wiley:2041210X:media:mee3261:mee3261-matematika-0077ke sejumlah level (atau faktor acak) yang sembarangan dalam kerangka Bayesian. Akan tetapi, implementasi umumnya agak sulit, dan oleh karena itu kami merujuk ke publikasi asli bagi mereka yang tertarik dengan metode ini.
Masalah ketiga dari generalisasi guci:x-wiley:2041210X:media:mee3261:mee3261-matematika-0078dan guci:x-wiley:2041210X:media:mee3261:mee3261-matematika-0079khususnya mendalam karena varians residual, guci:x-wiley:2041210X:media:mee3261:mee3261-matematika-0080, tidak dapat didefinisikan dengan mudah untuk respons non-Gaussian (lihat juga di bawah). Sekilas, mengadopsi ukuran R 2 berbasis kemungkinan seperti dalam Persamaan eqn 8-eqn 10 dapat menyelesaikan masalah ini meskipun metode tersebut hanya menyediakan R 2 pada tingkat unit (yaitu level 1); memang, jenis solusi ini telah direkomendasikan sebelumnya (Edwards et al . 2008 ). Sayangnya , ada tiga kendala dalam menggunakan R2 berbasis kemungkinan seperti untuk model umum: (i) kemungkinan tidak dapat dibandingkan ketika model dipasang dengan kemungkinan maksimum terbatas (REML) (cara standar untuk memperkirakan komponen varians dalam LMM; Pinheiro & Bates 2000 ), (ii) tidak jelas apakah kita harus menggunakan kemungkinan dari model nol seperti y ij = β 0 + ε ij (tidak termasuk faktor acak) atau dari model nol seperti y ij = β 0 + α j + ε ij (termasuk faktor acak; lihat Persamaan eqn 10 ) dan (iii) ukuran R2 berbasis kemungkinan yang diterapkan pada LMM dan GLMM juga tunduk pada masalah R2 yang menurun atau bahkan negatif dengan diperkenalkannya prediktor tambahan. Kami tidak mengetahui adanya solusi untuk kendala terakhir ini, tetapi solusi parsial untuk kendala (i) dan (ii) telah disarankan dan perlu dibahas secara terpisah.guci:x-wiley:2041210X:media:mee3261:mee3261-matematika-0081
Kendala pertama dalam pemasangan model dengan REML hanya berlaku untuk LMM, dan ini dapat diatasi dengan menggunakan estimasi ML alih-alih REML. Akan tetapi, sudah diketahui bahwa komponen varians akan bias ketika model dipasang dengan ML (misalnya Pinheiro & Bates 2000 ).
Mengenai kendala kedua mengenai pilihan model nol, tampaknya keduanya diizinkan dan diterima dalam literatur (misalnya Xu 2003 ; Orelien & Edwards 2008 ). Namun, penyertaan faktor acak dalam model intersep tentu dapat mengubah kemungkinan model nol yang digunakan sebagai referensi, dan dengan demikian, mengubah nilai R 2 . Ini terkait dengan masalah penting. Untuk model efek campuran, R 2 dapat dikategorikan secara longgar menjadi dua jenis: R 2 marginal dan R 2 kondisional (Vonesh, Chinchilli & Pu 1996 ). R 2 marginal berkaitan dengan varians yang dijelaskan oleh faktor-faktor tetap, dan R 2 kondisional berkaitan dengan varians yang dijelaskan oleh faktor-faktor tetap dan acak. Sejauh ini, kami hanya berkonsentrasi pada yang pertama, R 2 marginal , tetapi kami akan menguraikan lebih lanjut tentang perbedaan antara kedua jenis tersebut di bagian berikutnya.
Meskipun kami tidak meninjau semua definisi R 2 yang diusulkan untuk model efek campuran di sini (lihat Menard 2000 ; Xu 2003 ; Orelien & Edwards 2008 ; Roberts et al . 2011 ), tampaknya semua definisi alternatif R 2 mengalami satu atau lebih masalah yang disebutkan di atas dan implementasinya mungkin tidak mudah. Di bagian berikutnya, kami memperkenalkan definisi R 2 , yang sederhana dan umum untuk LMM dan GLMM dan mungkin kurang rentan terhadap masalah yang disebutkan di atas daripada definisi yang diusulkan sebelumnya.
R 2 umum dan sederhana untuk GLMM
Pertama-tama kita tinjau kembali poin bahwa varians yang dijelaskan ( guci:x-wiley:2041210X:media:mee3261:mee3261-matematika-0082) sebenarnya didefinisikan melalui varians yang tidak dijelaskan oleh model, dan sekarang kita mendefinisikannya kembali guci:x-wiley:2041210X:media:mee3261:mee3261-matematika-0083secara lebih langsung dalam hal varians yang dijelaskan:
guci:x-wiley:2041210X:media:mee3261:mee3261-matematika-0084
(persamaan 20)
guci:x-wiley:2041210X:media:mee3261:mee3261-matematika-0085
(persamaan 21)
di mana notasinya seperti pada Persamaan persamaan 3-persamaan 6. Di bawah ini, kami memperluas formulasi yang lebih langsung ini terlebih dahulu ke LMM dan kemudian ke GLMM. Untuk penyederhanaan, kami menggunakan LMM dengan dua faktor acak sebagai contoh. Demi ilustrasi, asumsikan bahwa dua efek acak adalah ‘kelompok’ (dengan individu yang secara unik ditetapkan ke dalam kelompok) dan ‘individu’ (dengan beberapa observasi per individu) (lih Persamaan persamaan 11-persamaan 13 ). Dengan demikian, observasi dikelompokkan dalam individu, dan individu bersarang dalam kelompok (lihat Schielzeth & Nakagawa 2012 untuk pembahasan tentang bersarang dalam model campuran). Model tersebut dapat ditulis sebagai:
guci:x-wiley:2041210X:media:mee3261:mee3261-matematika-0086
(persamaan 22)
guci:x-wiley:2041210X:media:mee3261:mee3261-matematika-0087
(persamaan 23)
guci:x-wiley:2041210X:media:mee3261:mee3261-matematika-0088
(persamaan 24)
guci:x-wiley:2041210X:media:mee3261:mee3261-matematika-0089
(persamaan 25)
di mana y ijk adalah respons ke – i dari individu ke- j , yang termasuk dalam kelompok ke -k , x hijk adalah nilai ke -i dari individu ke -j dalam kelompok ke -k untuk prediktor ke- h , γ k adalah efek khusus kelompok dari distribusi normal efek khusus kelompok dengan rata-rata nol dan varians guci:x-wiley:2041210X:media:mee3261:mee3261-matematika-0090, α jk adalah efek khusus individu dari distribusi normal efek khusus individu dengan rata-rata nol dan varians , guci:x-wiley:2041210X:media:mee3261:mee3261-matematika-0091dan ε ijk adalah residual dari distribusi normal efek khusus kelompok dengan rata-rata nol dan varians guci:x-wiley:2041210X:media:mee3261:mee3261-matematika-0092. R 2 untuk LMM yang diberikan oleh Persamaan persamaan 22 dapat didefinisikan sebagai:
guci:x-wiley:2041210X:media:mee3261:mee3261-matematika-0093
(persamaan 26)
guci:x-wiley:2041210X:media:mee3261:mee3261-matematika-0094
(persamaan 27)
di mana guci:x-wiley:2041210X:media:mee3261:mee3261-matematika-0095adalah varians yang dihitung dari komponen efek tetap LMM (lih. Snijders & Bosker 1999 ), m dalam tanda kurung menunjukkan R 2 marginal (yaitu varians yang dijelaskan oleh faktor-faktor tetap; lihat di bawah untuk R 2 bersyarat ). Estimasi guci:x-wiley:2041210X:media:mee3261:mee3261-matematika-0096, pada prinsipnya, dapat dilakukan dengan memperkirakan nilai-nilai yang disesuaikan berdasarkan efek-efek tetap saja (setara dengan mengalikan matriks desain efek-efek tetap dengan vektor estimasi efek tetap) diikuti dengan menghitung varians dari nilai-nilai yang disesuaikan ini (Snijders & Bosker 1999 ). Perhatikan bahwa guci:x-wiley:2041210X:media:mee3261:mee3261-matematika-0097harus diestimasi tanpa koreksi derajat kebebasan.
Keuntungan yang jelas dari formulasi ini adalah guci:x-wiley:2041210X:media:mee3261:mee3261-matematika-0098tidak akan pernah negatif. Ada kemungkinan bahwa guci:x-wiley:2041210X:media:mee3261:mee3261-matematika-0099dapat berkurang dengan penambahan prediktor (ingat bahwa guci:x-wiley:2041210X:media:mee3261:mee3261-matematika-0100tidak akan pernah berkurang dengan lebih banyak prediktor), tetapi ini tidak mungkin, karena guci:x-wiley:2041210X:media:mee3261:mee3261-matematika-0101harus selalu meningkat ketika prediktor ditambahkan ke model (bandingkan Persamaan 16 dan 26).
Bahasa Indonesia : Sekarang kita generalisasikan guci:x-wiley:2041210X:media:mee3261:mee3261-matematika-0102ke GLMM. Kami telah menyebutkan sebelumnya bahwa untuk respons non-Gaussian, sulit untuk mendefinisikan varians residual, guci:x-wiley:2041210X:media:mee3261:mee3261-matematika-0103. Namun, adalah mungkin untuk mendefinisikan varians residual pada skala laten (atau tautan), meskipun definisi varians residual ini khusus untuk distribusi kesalahan dan fungsi tautan yang digunakan dalam analisis. Dalam GLMM, guci:x-wiley:2041210X:media:mee3261:mee3261-matematika-0104dapat dinyatakan sebagai tiga komponen: (i) dispersi perkalian ( ω ), (ii) dispersi aditif ( guci:x-wiley:2041210X:media:mee3261:mee3261-matematika-0105) dan (iii) varians spesifik distribusi ( guci:x-wiley:2041210X:media:mee3261:mee3261-matematika-0106) (dirinci dalam Nakagawa & Schielzeth 2010 ). GLMM dapat diimplementasikan dalam dua cara berbeda, baik dengan dispersi perkalian atau aditif; dispersi disesuaikan untuk memperhitungkan varians yang melebihi atau kurang dari varians spesifik distribusi (misalnya dari distribusi binomial atau Poisson). Dalam makalah ini, kami hanya mempertimbangkan penerapan dispersi aditif GLMM meskipun rumus yang kami sajikan di bawah ini dapat dengan mudah dimodifikasi untuk penggunaan dengan GLMM yang berlaku untuk dispersi perkalian. Untuk detail lebih lanjut dan juga untuk tinjauan korelasi intra-kelas (juga dikenal sebagai pengulangan) dan heritabilitas, yang keduanya terkait erat dengan R 2 (lihat Nakagawa & Schielzeth 2010 ). Ketika dispersi aditif digunakan, guci:x-wiley:2041210X:media:mee3261:mee3261-matematika-0107sama dengan jumlah komponen dispersi aditif dan varians spesifik distribusi guci:x-wiley:2041210X:media:mee3261:mee3261-matematika-0108, dan dengan demikian, R 2 untuk GLMM dapat didefinisikan sebagai:
guci:x-wiley:2041210X:media:mee3261:mee3261-matematika-0109
(persamaan 28)
di mana guci:x-wiley:2041210X:media:mee3261:mee3261-matematika-0110varians dijelaskan pada skala laten (atau tautan) dan bukan pada skala asli. Hal ini dapat dengan mudah digeneralisasi ke beberapa tingkatan:
guci:x-wiley:2041210X:media:mee3261:mee3261-matematika-0111
(persamaan 29)
di mana u adalah jumlah faktor acak dalam GLMM (atau LMM) dan guci:x-wiley:2041210X:media:mee3261:mee3261-matematika-0112adalah komponen varians dari faktor acak ke -l . Persamaan 29 dapat dimodifikasi untuk menyatakan R 2 bersyarat (yaitu varians yang dijelaskan oleh faktor tetap dan acak).
guci:x-wiley:2041210X:media:mee3261:mee3261-matematika-0113
(persamaan 30)
Seperti yang dapat dilihat pada Persamaan 30 , R 2 bersyarat ( guci:x-wiley:2041210X:media:mee3261:mee3261-matematika-0114) meskipun namanya agak membingungkan dapat diartikan sebagai varians yang dijelaskan oleh keseluruhan model. Baik marginal maupun bersyarat guci:x-wiley:2041210X:media:mee3261:mee3261-matematika-0115menyampaikan informasi yang unik dan menarik, dan kami sarankan keduanya disajikan dalam publikasi.
Dalam kasus respons Gaussian dan tautan identitas (seperti yang digunakan dalam LMM), varians skala tertaut dan varians skala asli adalah sama dan varians spesifik distribusi adalah nol. Jadi, ( guci:x-wiley:2041210X:media:mee3261:mee3261-matematika-0116) direduksi menjadi guci:x-wiley:2041210X:media:mee3261:mee3261-matematika-0117dalam Persamaan persamaan 29 dan persamaan 30 . Untuk GLMM lain, varians skala tautan akan berbeda dari varians skala asli. Di sini kami menyajikan R 2 yang dihitung pada skala tautan karena sifatnya yang umum: Persamaan persamaan 29 dan persamaan 30 dapat diterapkan ke berbagai keluarga GLMM, dengan pengetahuan tentang varians spesifik distribusi guci:x-wiley:2041210X:media:mee3261:mee3261-matematika-0118dan model yang sesuai dengan overdispersi aditif (misalnya MCMCglmm; Hadfield 2010 ). Yang penting, ketika penyebut Persamaan persamaan 29 dan persamaan 30 mencakup guci:x-wiley:2041210X:media:mee3261:mee3261-matematika-0119(yaitu untuk GLMM), kedua jenis tidak akan pernah menjadi 1 yang kontras dengan R 2guci:x-wiley:2041210X:media:mee3261:mee3261-matematika-0120 tradisional (lihat juga Tabel 1 ). Tabel 2 merangkum spesifikasi untuk data biner/proporsi dan data hitungan, yang setara dengan Persamaan eqn 22-eqn 25. Rumusan GLMM yang disajikan dalam Tabel 2 untuk GLMM binomial pertama kali disajikan oleh Snijders & Bosker ( 1999 ). Mereka juga menunjukkan bahwa pendekatan ini dapat diperluas ke GLMM multinomial di mana responsnya kategoris dengan lebih dari dua level (Snijders & Bosker 1999 ; lihat juga Dean, Nakagawa & Pizzari 2011 ). Namun, sejauh pengetahuan kami, rumus yang setara untuk GLMM Poisson (yaitu data hitungan) belum pernah dijelaskan sebelumnya (untuk derivasi, lihat Lampiran 1).
Tabel 2. Contoh model linier campuran umum (GLMM) dengan kesalahan binomial dan Poisson (dua faktor acak) dan R 2 marginal dan kondisional yang sesuai
Data biner dan proporsi Hitung data
Fungsi tautan Tautan Logit Tautan Probit Tautan log Tautan akar kuadrat
Varians spesifik distribusi guci:x-wiley:2041210X:media:mee3261:mee3261-matematika-0121 1 guci:x-wiley:2041210X:media:mee3261:mee3261-matematika-0122 0,25
Spesifikasi model
guci:x-wiley:2041210X:media:mee3261:mee3261-matematika-0123
guci:x-wiley:2041210X:media:mee3261:mee3261-matematika-0124
guci:x-wiley:2041210X:media:mee3261:mee3261-matematika-0125
guci:x-wiley:2041210X:media:mee3261:mee3261-matematika-0126
guci:x-wiley:2041210X:media:mee3261:mee3261-matematika-0127
guci:x-wiley:2041210X:media:mee3261:mee3261-matematika-0128
guci:x-wiley:2041210X:media:mee3261:mee3261-matematika-0129
guci:x-wiley:2041210X:media:mee3261:mee3261-matematika-0130
guci:x-wiley:2041210X:media:mee3261:mee3261-matematika-0131
guci:x-wiley:2041210X:media:mee3261:mee3261-matematika-0132
Keterangan Y ijk adalah jumlah ‘keberhasilan’ dalam percobaan m ijk oleh individu ke -j dalam kelompok ke – k pada kesempatan ke – i (untuk data biner, m ijk adalah 1), p ijk adalah probabilitas dasar (laten) keberhasilan bagi individu ke -j dalam kelompok ke -k pada kesempatan ke – i (untuk data biner, guci:x-wiley:2041210X:media:mee3261:mee3261-matematika-0133adalah 0). Y ijk merupakan hitungan teramati untuk individu ke -j dalam kelompok ke- k pada kesempatan ke – i, μ ijk merupakan rata-rata mendasar (laten) untuk individu ke – i dalam kelompok ke -k pada kesempatan ke – i.
Marjinal R 2 guci:x-wiley:2041210X:media:mee3261:mee3261-matematika-0134 guci:x-wiley:2041210X:media:mee3261:mee3261-matematika-0135 guci:x-wiley:2041210X:media:mee3261:mee3261-matematika-0136 guci:x-wiley:2041210X:media:mee3261:mee3261-matematika-0137 guci:x-wiley:2041210X:media:mee3261:mee3261-matematika-0138
Kondisional R 2 guci:x-wiley:2041210X:media:mee3261:mee3261-matematika-0139 guci:x-wiley:2041210X:media:mee3261:mee3261-matematika-0140 guci:x-wiley:2041210X:media:mee3261:mee3261-matematika-0141 guci:x-wiley:2041210X:media:mee3261:mee3261-matematika-0142 guci:x-wiley:2041210X:media:mee3261:mee3261-matematika-0143
Sebagai catatan teknis, kami sebutkan bahwa untuk data biner, overdispersi aditif biasanya ditetapkan ke 1 untuk alasan komputasi, karena dispersi aditif tidak dapat diidentifikasi (lihat Goldstein, Browne & Rasbash 2002 ). Lebih jauh, beberapa rumus R 2 menyertakan intersep β 0 (seperti dalam kasus model Poisson untuk data hitungan). Dalam kasus seperti itu, nilai R 2 akan lebih mudah ditafsirkan ketika efek tetap dipusatkan atau memiliki nilai nol yang bermakna (lihat Schielzeth 2010 ; lihat juga Lampiran 1). Kami selanjutnya mencatat bahwa untuk model Poisson dengan tautan akar kuadrat dan rata-rata Y ijk <5, rumus yang diberikan cenderung tidak akurat karena varians transformasi akar kuadrat dari data hitungan secara substansial melebihi 0·25 (Tabel 2 ; Nakagawa & Schielzeth 2010 ).
Masalah terkait
Meskipun keuntungan yang jelas dari penggunaan guci:x-wiley:2041210X:media:mee3261:mee3261-matematika-0144adalah kesederhanaannya, satu kekurangannya adalah guci:x-wiley:2041210X:media:mee3261:mee3261-matematika-0145tidak menyediakan informasi mengenai varians yang dijelaskan pada setiap level dengan cara yang dilakukan guci:x-wiley:2041210X:media:mee3261:mee3261-matematika-0146dan guci:x-wiley:2041210X:media:mee3261:mee3261-matematika-0147. Kekurangan ini dapat diperbaiki dengan menyediakan perubahan proporsi dalam varians (PCV; Merlo et al . 2005a , b ) sebagai informasi pendukung dalam publikasi. Dengan menggunakan Persamaan eqn 22-eqn 25 , PCV pada tiga level yang berbeda dapat dinyatakan sebagai:
guci:x-wiley:2041210X:media:mee3261:mee3261-matematika-0148
(persamaan 31)
guci:x-wiley:2041210X:media:mee3261:mee3261-matematika-0149
(persamaan 32)
guci:x-wiley:2041210X:media:mee3261:mee3261-matematika-0150
(persamaan 33)
di mana C γ , C α dan C ɛ adalah PCV pada tingkat kelompok, individu dan unit (observasi), masing-masing, dan guci:x-wiley:2041210X:media:mee3261:mee3261-matematika-0151, guci:x-wiley:2041210X:media:mee3261:mee3261-matematika-0152dan guci:x-wiley:2041210X:media:mee3261:mee3261-matematika-0153adalah komponen varians dari model intersep (yaitu Persamaan eqn 22 ; PCV untuk dispersi aditif, guci:x-wiley:2041210X:media:mee3261:mee3261-matematika-0154juga dapat dihitung dengan mengganti guci:x-wiley:2041210X:media:mee3261:mee3261-matematika-0155dengan guci:x-wiley:2041210X:media:mee3261:mee3261-matematika-0156). Perubahan proporsi dalam varians sebenarnya adalah salah satu ukuran R 2 yang diusulkan paling awal untuk LMM (Raudenbush & Bryk 1986 ; Bryk & Raudenbush 1992 ), meskipun dapat mengambil nilai negatif (Snijders & Bosker 1994 ). Namun, kami pikir bahwa menyajikan PCV bersama dengan R 2 GLMM akan menjadi sangat berguna, karena PCV memantau perubahan yang spesifik untuk setiap komponen varians, yaitu, bagaimana penyertaan prediktor tambahan telah mengurangi (atau meningkatkan) komponen varians pada tingkat yang berbeda. Misalnya, jika C γ = 0·12, C α = −0·05 dan C ɛ = 0·23, estimasi negatif menunjukkan bahwa varians pada tingkat individu telah meningkat (yaitu guci:x-wiley:2041210X:media:mee3261:mee3261-matematika-0157). Selain itu, kami merujuk pembaca ke Hössjer ( 2008 ) yang menjelaskan pendekatan alternatif untuk mengukur varians yang dijelaskan pada berbagai tingkat menggunakan komponen varians dari satu model.
Sejauh ini, kita hanya membahas model intersep acak (misalnya Persamaan 22 ) bukan model kemiringan acak di mana kemiringan disesuaikan untuk setiap kelompok (biasanya bersama dengan intersep acak pada setiap level; lihat Schielzeth & Forstmeier ( 2009 ) yang menyoroti perlunya menyesuaikan model kemiringan acak ketika minat utamanya adalah pada prediktor efek tetap level data). Snijders & Bosker ( 1999 ) menunjukkan bahwa menghitung R2 seperti dan , mudah dilakukan untuk model intersep acak, tetapi untuk model kemiringan acak itu membosankan (karena komponen varians untuk kemiringan tidak dapat dengan mudah diintegrasikan dengan komponen varians lainnya, misalnya Schielzeth & Forstmeier 2009 ). Snijders & Bosker ( 1999 ) menyebutkan bahwa dan yang diperoleh dari model kemiringan acak biasanya sangat mirip dengan yang diperoleh dari model intersep acak, di mana efek tetap yang sama disesuaikan. Oleh karena itu, kami sarankan melakukan perhitungan (baik marginal maupun kondisional) dari model intersep acak yang sesuai untuk model kemiringan acak, meskipun PCV harus dihitung untuk model kemiringan acak yang diinginkan.guci:x-wiley:2041210X:media:mee3261:mee3261-matematika-0158guci:x-wiley:2041210X:media:mee3261:mee3261-matematika-0159guci:x-wiley:2041210X:media:mee3261:mee3261-matematika-0160guci:x-wiley:2041210X:media:mee3261:mee3261-matematika-0161guci:x-wiley:2041210X:media:mee3261:mee3261-matematika-0162
Contoh yang dikerjakan
Kami akan mengilustrasikan bagaimana perhitungan guci:x-wiley:2041210X:media:mee3261:mee3261-matematika-0163bersama dengan PCV menggunakan kumpulan data simulasi. Pertimbangkan spesies kumbang hipotetis yang memiliki siklus hidup berikut: larva menetas dan tumbuh di tanah hingga menjadi kepompong, dan kemudian kumbang dewasa makan dan kawin pada tanaman. Mereka adalah spesies generalis dan tersebar luas. Kami tertarik pada efek nutrisi tambahan selama tahap larva pada morfologi dan keberhasilan reproduksi berikutnya. Larva diambil sampelnya dari 12 populasi berbeda (‘Populasi’; lihat Gambar 1 ). Dalam setiap populasi, larva dikumpulkan di dua mikrohabitat berbeda (‘Habitat’): daerah kering dan basah sebagaimana ditentukan oleh kelembaban tanah. Larva terkena dua perlakuan diet yang berbeda (‘Perlakuan’): kaya nutrisi dan kontrol. Spesies ini dimorfik seksual dan dapat dengan mudah ditentukan jenis kelaminnya pada tahap pupa (‘Jenis Kelamin’). Kumbang jantan memiliki dua morf warna yang berbeda: satu gelap dan yang lainnya coklat kemerahan (‘Morf’, berlabel A dan B pada Gambar 1 ), dan morf tersebut seharusnya tunduk pada seleksi seksual. Pupa yang sudah dibedakan jenis kelaminnya ditempatkan dalam wadah standar hingga mereka dewasa (‘Wadah’). Setiap wadah menampung delapan hewan berjenis kelamin sama dari satu populasi, tetapi dengan campuran individu dari dua habitat ( N [wadah] = 120; N [hewan] = 960). Tiga sifat diukur setelah pematangan: (i) panjang tubuh kumbang dewasa (distribusi Gaussian), (ii) frekuensi dua morf warna jantan yang berbeda (distribusi binomial atau Bernoulli) dan (iii) jumlah telur yang diletakkan oleh setiap betina (distribusi Poisson) setelah perkawinan acak (Gbr. 1 ).
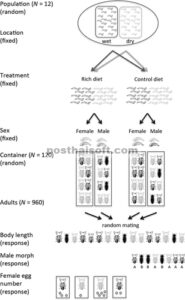
Skema bagaimana himpunan data hipotetis diperoleh (lihat teks utama untuk detailnya).
Data untuk contoh hipotetis ini dibuat dalam R 2.15.0 (Tim Inti Pengembangan R 2012 ). Kami menggunakan fungsi lmer dalam paket R lme4 (versi 0.999375-42; Bates, Maechler & Bolker 2011 ) untuk menyesuaikan LMM dan GLMM. Kami memodelkan tiga variabel respons (lihat juga Tabel 3 ): (i) panjang tubuh dengan kesalahan Gaussian (‘Model ukuran’), (ii) dua morf jantan dengan kesalahan binomial (fungsi tautan logit; ‘Model morf’) dan (iii) jumlah telur betina dengan kesalahan Poisson (fungsi tautan log; ‘Model kesuburan’). Untuk setiap kumpulan data, kami menyesuaikan model null (intersep/kosong) dan model ‘penuh’; semua model berisi ‘Populasi’ dan ‘Wadah’ sebagai faktor acak; kami menyertakan istilah dispersi aditif (lihat Tabel 2 ) dalam model Kesuburan. Semua model lengkap menyertakan ‘Perawatan’ dan ‘Habitat’ sebagai faktor tetap; ‘Jenis Kelamin’ ditambahkan sebagai faktor tetap pada model ukuran tubuh. Dua jenis guci:x-wiley:2041210X:media:mee3261:mee3261-matematika-0164dan PCV untuk tiga komponen varians dihitung seperti yang dijelaskan di atas. Hasil pemodelan tiga set data yang berbeda dirangkum dalam Tabel 3 ; semua set data dan skrip R disediakan sebagai suplemen daring (Data S1-4).
Tabel 3. Pemodelan efek campuran hipotetis dari pengaruh manipulasi nutrisi terhadap panjang tubuh (mm) (Model ukuran), morfologi jantan (Model morf) dan sel telur betina (Model kesuburan); N [populasi] = 12, N [wadah] = 120 dan N [hewan] = 960
Nama model Model ukuran Model campuran Gaussian Model Morph Model campuran biner (tautan logit) Model kesuburan Model campuran Poisson (tautan log)
Model Nol Model Lengkap Model Nol Model Lengkap Model Nol Model Lengkap
Efek tetap b [95% CI] b [95% CI] b [95% CI] b [95% CI] b [95% CI] b [95% CI]
Mencegat tanggal 14·08 [13·41, 14·76] 15·22 [14·53, 15·91] -0·38 [-0·96, 0·21] -1·25 [-1·96, -0·54] 1·54 [1·22, 1·86] 1·23 [0·91, 1·56]
Perawatan (eksperimen) – 0·31 [0·18, 0·45] – 1·01 [0·60, 1·43] – 0·51 [0·41, 0·26]
Habitat (basah) – 0·09 [−0·05, 0·23] – 0·68 [0·27, 1·09] – 0·10 [0·001, 0·20]
Jenis Kelamin (laki-laki) – -2·66 [-2·89, -2·45] – – – –
Efek acak VC VC VC VC VC VC
Populasi 1·181 1·379 0·946 1·110 0,303 0,304
Wadah 2.206 tahun 0,235 < 0·0001 0,006 0,012 0,023
Residu (dispersi aditif) 1.224 tahun 1 tahun 197 – – 0·171 0,100
Faktor Tetap – 1·809 – 0·371 – 0,067
PCV [Populasi] – -16,77% – -17,34% – -0,54%
PCV [Kontainer] – 89,37% – <−100% – -84,32%
PCV [Sisa] – 2,21% – – – 41,54%
guci:x-wiley:2041210X:media:mee3261:mee3261-matematika-0165 – 39,16% – 7,77% – 9,76%
guci:x-wiley:2041210X:media:mee3261:mee3261-matematika-0166 – 74,09% – 31,13% – 57,23%
AIK 3275 3063 602·4 573·1 902·7 811·9
BIC 3295 3097 614·9 594·0 920·4 836·9
CI, interval kepercayaan; PCV, perubahan proporsi dalam varians; NA, tidak berlaku/tersedia; AIC, Kriteria Informasi Akaike; BIC; Kriteria informasi Bayesian; ML, kemungkinan maksimum; REML, kemungkinan maksimum terbatas; VC, komponen varians.
Untuk model lengkap, intersep mewakili kontrol, kering, dan betina. 95% CI diestimasikan dengan mengasumsikan derajat kebebasan yang sangat besar (yaitu t = 1·96). Untuk model Ukuran, nilai AIC dan BIC dihitung menggunakan ML tetapi parameter lainnya berasal dari estimasi REML (lihat teks untuk alasannya).
Dalam ketiga set model, beberapa komponen varians dalam model lengkap lebih besar daripada komponen varians yang sesuai dalam model nol (misalnya guci:x-wiley:2041210X:media:mee3261:mee3261-matematika-0167). Dalam model Morph, jumlah semua komponen varians efek acak dalam model lengkap lebih besar daripada total varians dalam model nol (lih guci:x-wiley:2041210X:media:mee3261:mee3261-matematika-0168); lihat di atas; Snijders & Bosker 1994 ). Semua pola ini menghasilkan nilai PCV negatif (lihat Tabel 3 ), sementara guci:x-wiley:2041210X:media:mee3261:mee3261-matematika-0169nilai tidak pernah menjadi negatif. Dalam model Morph dan Fecundity, guci:x-wiley:2041210X:media:mee3261:mee3261-matematika-0170nilai relatif minor (8–10%) dibandingkan dengan guci:x-wiley:2041210X:media:mee3261:mee3261-matematika-0171nilai. Dalam model Size, di sisi lain, guci:x-wiley:2041210X:media:mee3261:mee3261-matematika-0172hampir 40%. Hal ini disebabkan oleh efek ‘Sex’ yang sangat besar dalam model ukuran tubuh; dalam model ini, efek ‘Treatment’ dan ‘Habitat’ bersama-sama hanya mencakup c . 1% dari varians (tidak ditampilkan dalam Tabel 3 ). Varians di antara kontainer dalam model Ukuran nol digabungkan dengan varians yang disebabkan oleh perbedaan antara jenis kelamin dalam model nol, karena ‘Jenis Kelamin’ dan ‘Kontainer’ dikacaukan oleh desain eksperimen (jenis kelamin tunggal di setiap kontainer; Gambar 1 ). Sebagian dari variasi yang ditetapkan untuk ‘Kontainer’ dalam model nol dijelaskan oleh efek tetap ‘Jenis Kelamin’ dalam model lengkap. Akhirnya, penting untuk dicatat bahwa efek ‘Perlakuan’ dan ‘Habitat’ secara statistik signifikan dalam semua kumpulan data dalam banyak kasus (lima dari enam). Namun, sebagian besar variabilitas data berada dalam efek acak bersama dengan residual (dispersi aditif) dan dalam varians spesifik distribusi. Perhatikan bahwa perbedaan antara nilai yang sesuai guci:x-wiley:2041210X:media:mee3261:mee3261-matematika-0173dan guci:x-wiley:2041210X:media:mee3261:mee3261-matematika-0174mencerminkan seberapa banyak variabilitas dalam efek acak. Yang penting, membandingkan komponen varians yang berbeda termasuk faktor tetap dalam maupun antara model, kami percaya, dapat membantu peneliti mendapatkan wawasan tambahan ke dalam kumpulan data mereka (Merlo et al . 2005a , b ). Kami juga mencatat bahwa dalam beberapa kasus, menghitung komponen varians untuk setiap faktor tetap mungkin terbukti berguna.
Catatan akhir
Di sini, kami telah menyediakan ukuran umum R 2 yang kami beri label guci:x-wiley:2041210X:media:mee3261:mee3261-matematika-0175. Baik marginal maupun kondisional guci:x-wiley:2041210X:media:mee3261:mee3261-matematika-0176dapat dengan mudah dihitung, terlepas dari paket statistik yang digunakan untuk menyesuaikan model. Meskipun kami tidak mengklaim bahwa guci:x-wiley:2041210X:media:mee3261:mee3261-matematika-0177adalah statistik ringkasan yang sempurna, statistik tersebut kurang rentan terhadap masalah umum yang mengganggu ukuran alternatif R 2 . Kami lebih lanjut percaya bahwa guci:x-wiley:2041210X:media:mee3261:mee3261-matematika-0178dapat digunakan sebagai kuantitas kepentingan biologis dan karenanya guci:x-wiley:2041210X:media:mee3261:mee3261-matematika-0179dapat dianggap sebagai yang diestimasi dari data daripada dihitung untuk kumpulan data tertentu. Kegunaan empiris guci:x-wiley:2041210X:media:mee3261:mee3261-matematika-0180sebagai penduga varians yang dijelaskan masih harus diuji dalam penelitian mendatang. Seperti halnya setiap penduga kepentingan biologis, diinginkan untuk mengkuantifikasi ketidakpastian di sekitar estimasi ini (misalnya interval kepercayaan 95%, yang dapat diperkirakan dengan bootstrapping parametrik atau pengambilan sampel MCMC). Sejauh yang kami ketahui, estimasi ketidakpastian tersebut belum dipertimbangkan untuk R 2 tradisional . Mungkin, penelitian mendatang juga dapat menyelidiki kegunaan estimasi ketidakpastian untuk dan pengukuran R 2guci:x-wiley:2041210X:media:mee3261:mee3261-matematika-0181 lainnya .
Kami akhiri dengan catatan peringatan bahwa R2 tidak boleh menggantikan penilaian model seperti pemeriksaan diagnostik untuk heteroskedastisitas, memvalidasi asumsi pada distribusi efek acak dan analisis outlier. Di atas, kami menyajikan R2 dengan motivasi meringkas jumlah varians yang dijelaskan dalam model yang cocok untuk pertanyaan penelitian dan kumpulan data tertentu. Ini hanya boleh digunakan pada model yang telah diperiksa kualitasnya dengan cara lain. Penting juga untuk menyadari bahwa R2 bisa menjadi besar karena prediktor yang tidak memiliki minat langsung dalam studi tertentu (Tjur 2009 ) seperti efek jenis kelamin pada ukuran tubuh dalam contoh kami. Meskipun ada keterbatasan ini, ketika digunakan bersama dengan statistik lain seperti AIC dan PCV, akan menjadi statistik ringkasan yang berguna dari model efek campuran baik untuk ahli biologi maupun ilmuwan lain.guci:x-wiley:2041210X:media:mee3261:mee3261-matematika-0182
Ucapan Terima Kasih
Kami berterima kasih kepada S. English, C. Grueber, F. Korner-Nievergelt, E. Santos, A. Senior, dan T. Uller atas komentar pada versi sebelumnya dan M. Lagisz atas bantuannya dalam menyiapkan Gambar 1. Kami juga berterima kasih kepada Editor R. O’Hara dan dua peninjau anonim, yang komentarnya telah menyempurnakan makalah ini. T. Snijders memberikan panduan tentang cara menghitung varians untuk efek tetap. HS didukung oleh beasiswa Emmy-Noether dari Yayasan Riset Jerman (SCHI 1188/1-1).
Lampiran 1
Turunan varians spesifik distribusi ( guci:x-wiley:2041210X:media:mee3261:mee3261-matematika-0183) untuk distribusi Poisson
Ketika variabel acak x berdistribusi Poisson, mean dan varians x berturut-turut adalah:
guci:x-wiley:2041210X:media:mee3261:mee3261-matematika-0184
(A1)
guci:x-wiley:2041210X:media:mee3261:mee3261-matematika-0185
(A2)
Distribusi ln( x ) dapat didekati dengan logaritma natural dari distribusi log-normal. Dengan demikian, varians ln( x ) dapat didekati sebagai:
guci:x-wiley:2041210X:media:mee3261:mee3261-matematika-0186
Bahasa Indonesia: (A3)
Dengan mensubstitusikan Persamaan A1 dan A2 ke Persamaan A3, kita memperoleh:
guci:x-wiley:2041210X:media:mee3261:mee3261-matematika-0187
Bahasa Indonesia: (A4)
Karena itu,
guci:x-wiley:2041210X:media:mee3261:mee3261-matematika-0188
Bahasa Indonesia: (A5)
Ketika kita mengganti var(ln( x )) dengan guci:x-wiley:2041210X:media:mee3261:mee3261-matematika-0189dan λ dengan exp(β 0 ), kita memperoleh:
guci:x-wiley:2041210X:media:mee3261:mee3261-matematika-0190
Bahasa Indonesia: (A6)
Simulasi (data yang tidak dipublikasikan, penulis) menunjukkan bahwa ketika E ( x ) mendekati 0, perkiraan ini menjadi tidak dapat diandalkan. Selain itu, exp(β 0 ) harus diperoleh baik dari model dengan variabel terpusat atau berskala ( sense Schielzeth 2010 ), atau model intersep saja sambil memasukkan semua efek acak. Perhatikan bahwa pendekatan sebelumnya mungkin terbatas ketika model menyertakan variabel kategoris.
